Excel SORT function - automatically sort with formula

Excel SORT function - tips and notes

SORT is a new dynamic array function and as such it has a couple of specificities that you should be aware of:

• Currently the SORT function is only available in Microsoft 365 and Excel 2021. Excel 2019, Excel 2016 do not support dynamic array formulas, so the SORT function is not available in these versions.
• If the array returned by a SORT formula is the final result (i.e. not passed to another function), Excel dynamically creates an appropriately sized range and populates it with the sorted values. So, be sure you always have enough empty cells down or/and to the right of the cell where you enter the formula, otherwise a #SPILL error occurs.
• The results update dynamically as the source data changes. However, the array supplied to the formula does not extend automatically to include new entries that are added outside of the referenced array. To include such items, you need to either update the array reference in your formula, or convert the source range to an table as shown in this example, or create a dynamic named range.

Formula to sort in ascending order

To sort values in column B from smallest to largest, here's the formula to use:

=SORT(A2:B8, 2, 1)

Where:

• A2:B8 is the source array
• 2 is the column number to sort by
• 1 is the ascending sort order

Since our data is organized in rows, the last argument can be omitted to default to FALSE - sort by rows.

Just enter the formula in any empty cell (D2 in our case), press Enter, and the results will spill automatically to D2:E8.

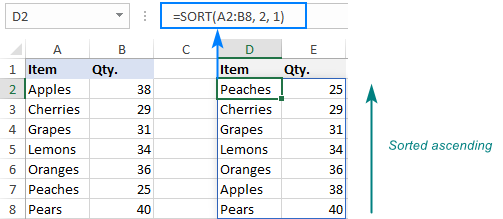
Formula to sort in descending order

To sort data descending, i.e. from largest to smallest, set the sort_order argument to -1 like this:

=SORT(A2:B8, 2, -1)

Enter the formula in the top left cell of the destination range and you will get this result:

In a similar manner, you can sort text values in alphabetical order from A to Z or from Z to A.

Excel SORT by column

When you sort data in Excel, for the most part you change the order of rows. But when your data is organized horizontally with rows containing labels and columns containing records, you might need to sort from left to right, rather than from top to bottom.

To sort by column in Excel, set the by_col argument to TRUE. In this case, sort_index will represent a row, not a column.

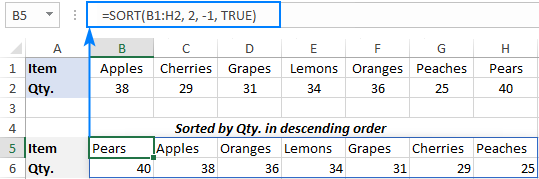
For example, to sort the below data by Qty. from highest to lowest, use this formula:

=SORT(B1:H2, 2, 1, TRUE)

Where:

• B1:H2 is the source data to sort
• 2 is the sort index, since we are sorting numbers in the second row
• -1 indicates the descending sort order
• TRUE means to sort columns, not rows

Sort by multiple columns in different order (multi-level sort)

When working with complex data models, you may often need a multi-level sort. Can that be done with a formula? Yep, easily! What you do is to supply array constants for the sort_index and sort_order arguments.

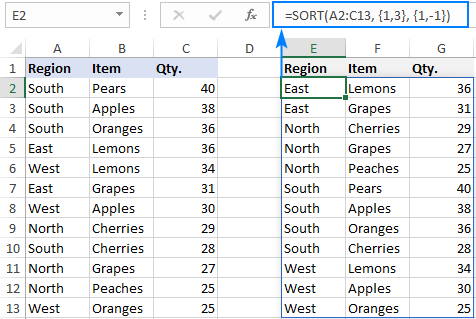
For example, to sort the below data first by Region (column A) from A to Z, and then by Qty. (column C) from smallest to largest, set the following arguments:

• Array is the data in A2:C13.
• Sort_index is the array constant {1,3}, since we first sort by Region (1^st column), and then by Qty. (3^rd column).
• Sort_order is the array constant {1,-1}, since the 1st column is to be sorted in ascending order and the 3^rd column in descending order.
• By_col is omitted because we sort rows, which is default.

Putting the arguments together, we get this formula:

=SORT(A2:C13, {1,3}, {1,-1})

And it works perfectly! The text values in the first column are sorted alphabetically and the numbers in the third column from largest to smallest:

Sort and filter in Excel

In case when you are looking to filter data with some criteria and put the output in order, use the SORT and FILTER functions together:

The FILTER function gets an array of values based on the criteria you define and passes that array to the first argument of SORT.

The best thing about this formula is that it also outputs the results as a dynamic spill range, without you having to press Ctrl + Shift + Enter or guess at how many cells to copy it to. As usual, you type a formula in the upper most cell and hit the Enter key.

As an example, we are going to extract items with quantity equal to or greater than 30 (>=30) from the source data in A2:B9 and arrange the results in ascending order.

For this, we first set up the condition, say, in cell E2 as shown in the image below. And then, build our Excel SORT formula in this way:

=SORT(FILTER(A2:B9, B2:B9>=E2), 2)

Apart from array generated by the FILTER function, we only specify the sort_index argument (column 2). The remaining two arguments are omitted because the defaults work exactly as we need (sort ascending, by row).

Get N largest or smallest values and sort the results

When analyzing huge bulks if information, there is often a need to extract a certain number of top values. Maybe not just extract, but also arrange them in the desired order. And ideally, choose which columns to include in the results. Sounds tricky? Not with the new dynamic array functions!

Here is a generic formula:

Where n is the number of the values you want to return.

From the below data set, assume you want to get a top 3 list based on the numbers in column C.

To have it done, you first sort the array A2:C13 by the 3^rd column in descending order:

SORT(A2:C13, 3, -1)

And then, nest the above formula in the first (array) argument of the INDEX function to have the array sorted from highest to smallest.

For the second (row_num) argument, which indicates how many rows to return, generate the required sequential numbers by using the SEQUENCE function. As we need 3 top values, we use SEQUENCE(3), which is the same as supplying a vertical array constant {1;2;3} directly in the formula.

For the third (col_num) argument, which defines how many columns to return, supply the column numbers in the form of a horizontal array constant. We want to return columns B and C, so we use the array {2,3}.

Eventually, we get the following formula:

=INDEX(SORT(A2:C13, 3, -1), SEQUENCE(3), {2,3})

And it produces exactly the results we want:

To return 3 bottom values, simply sort the original data from smallest to largest. For this, change the sort_order argument from -1 to 1:

=INDEX(SORT(A2:C13, 3, 1), SEQUENCE(3), {2,3})

Return a sorted value in a specific position

Looking from another angle, what if you only want to return a specific sort position? Say, only the 1st , only the 2nd, or only the 3rd record from the sorted list? To have it done, use the simplified version of the INDEX SORT formula discussed above:

Where n is the position of interest.

For example, to get a particular position from top (i.e. from the data sorted descending), use this formula:

=INDEX(SORT(A2:C13, 3, -1), F1, {2,3})

To get a specific position from bottom (i.e. from the data sorted ascending), use this one:

=INDEX(SORT(A2:C13, 3, 1), I1, {2,3})

Where A2:C13 is source data, F1 is the position from top, I1 is the position from bottom, and {2,3} are the columns to be returned.

#NAME error: older Excel version

SORT is a new function and works only in Excel 365 and Excel 2021. In older versions where this function is not supported, a #NAME? error occurs.

#SPILL error: something blocks spill range

If one or more cells in the spill range are not completely blank or merged, a #SPILL! error is displayed. To fix it, just remove the blockage. For more information, please see Excel #SPILL! error - what it means and how to fix.

#VALUE error: invalid arguments

Whenever you run into a #VALUE! error, check the sort_index and sort_order arguments. Sort_index should not exceed the number of columns is array, and sort_order should be either 1 (ascending) or -1 (descending).

#REF error: source workbook is closed

Since dynamic arrays have limited support for references between workbooks, the SORT function requires both files to be open. If the source workbook is closed, a formula will throw a #REF! error. To fix it, just open the referenced file.