by The tutorial shows how to build an amortization schedule in Excel to detail periodic payments on an amortizing loan or mortgage.
An amortizing loan is just a fancy way to define a loan that is paid back in installments throughout the entire term of the loan.
Basically, all loans are amortizing in one way or another. For example, a fully amortizing loan for 24 months will have 24 equal monthly payments. Each payment applies some amount towards principal and some towards interest. To detail each payment on a loan, you can build a loan amortization schedule.
An amortization schedule is a table that lists periodic payments on a loan or mortgage over time, breaks down each payment into principal and interest, and shows the remaining balance after each payment.
How to create a loan amortization schedule in Excel
To build a loan or mortgage amortization schedule in Excel, we will need to use the following functions:
- PMT function - calculates the total amount of a periodic payment. This amount stays constant for the entire duration of the loan.
- PPMT function - gets the principal part of each payment that goes toward the loan principal, i.e. the amount you borrowed. This amount increases for subsequent payments.
- IPMT function - finds the interest part of each payment that goes toward interest. This amount decreases with each payment.
Now, let's go through the process step-by-step.
1. Set up the amortization table
For starters, define the input cells where you will enter the known components of a loan:
- C2 - annual interest rate
- C3 - loan term in years
- C4 - number of payments per year
- C5 - loan amount
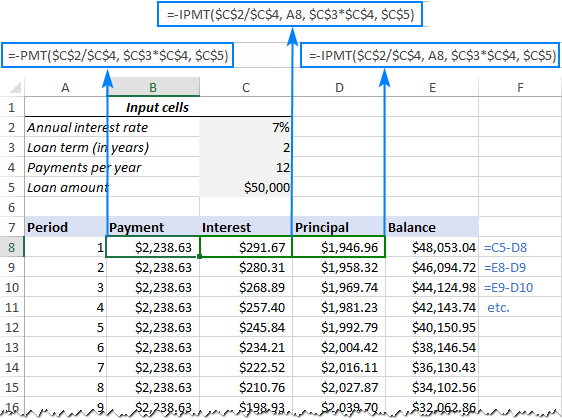
The next thing you do is to create an amortization table with the labels (Period, Payment, Interest, Principal, Balance) in A7:E7. In the Period column, enter a series of numbers equal to the total number of payments (1- 24 in this example):
With all the known components in place, let's get to the most interesting part - loan amortization formulas.
2. Calculate total payment amount (PMT formula)
The payment amount is calculated with the PMT(rate, nper, pv, [fv], [type]) function.
To handle different payment frequencies correctly (such as weekly, monthly, quarterly, etc.), you should be consistent with the values supplied for the rate and nper arguments:
- Rate - divide the annual interest rate by the number of payment periods per year ($C$2/$C$4).
- Nper - multiply the number of years by the number of payment periods per year ($C$3*$C$4).
- For the pv argument, enter the loan amount ($C$5).
- The fv and type arguments can be omitted since their default values work just fine for us (balance after the last payment is supposed to be 0; payments are made at the end of each period).
Putting the above arguments together, we get this formula:
=PMT($C$2/$C$4, $C$3*$C$4, $C$5)
Please pay attention, that we use absolute cell references because this formula should copy to the below cells without any changes.
Enter the PMT formula in B8, drag it down the column, and you will see a constant payment amount for all the periods:
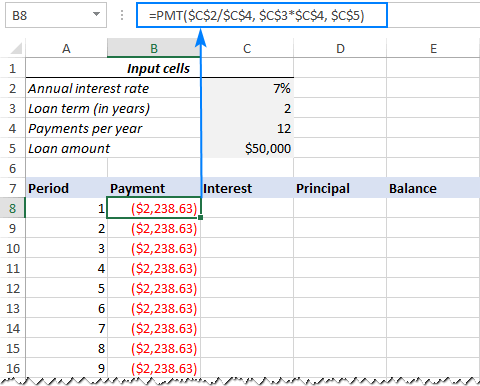
3. Calculate interest (IPMT formula)
To find the interest part of each periodic payment, use the IPMT(rate, per, nper, pv, [fv], [type]) function:
=IPMT($C$2/$C$4, A8, $C$3*$C$4, $C$5)
All the arguments are the same as in the PMT formula, except the per argument that specifies the payment period. This argument is supplied as a relative cell reference (A8) because it is supposed to change based on the relative position of a row to which the formula is copied.
This formula goes to C8, and then you copy it down to as many cells as needed:
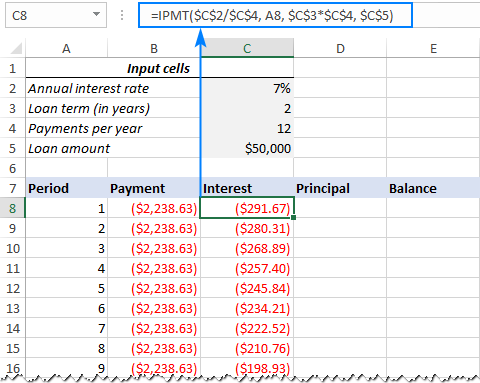
4. Find principal (PPMT formula)
To calculate the principal part of each periodic payment, use this PPMT formula:
=PPMT($C$2/$C$4, A8, $C$3*$C$4, $C$5)
The syntax and arguments are exactly the same as in the IPMT formula discussed above:
This formula goes to column D, beginning in D8:
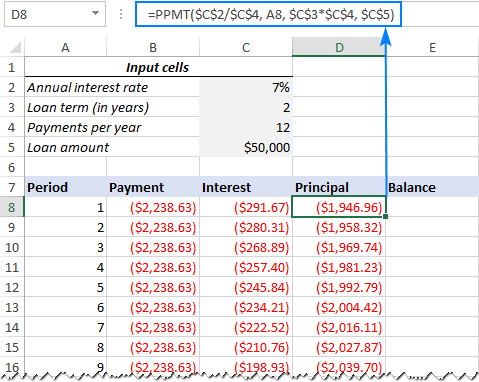
Tip. To check whether your calculations are correct at this point, add up the numbers in the Principal and Interest columns. The sum should be equal to the value in the Payment column in the same row.
5. Get the remaining balance
To calculate the remaining balance for each period, we'll be using two different formulas.
To find the balance after the first payment in E8, add up the loan amount (C5) and the principal of the first period (D8):
=C5+D8
Because the loan amount is a positive number and principal is a negative number, the latter is actually subtracted from the former.
For the second and all succeeding periods, add up the previous balance and this period's principal:
=E8+D9
The above formula goes to E9, and then you copy it down the column. Due to the use of relative cell references, the formula adjusts correctly for each row.
That's it! Our monthly loan amortization schedule is done:
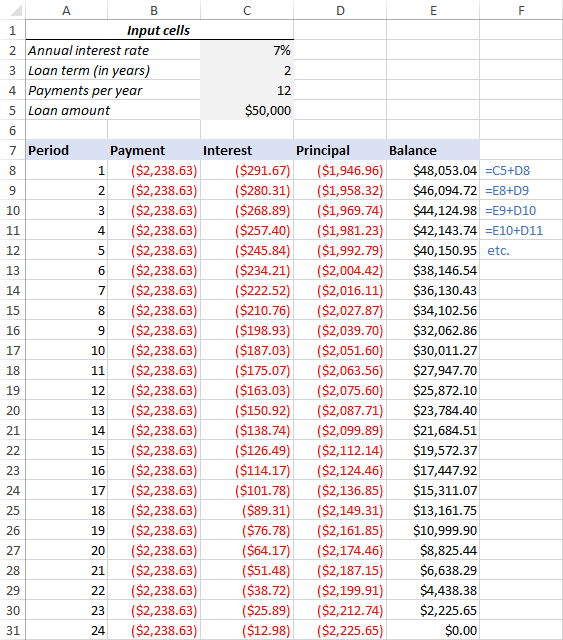
Tip: Return payments as positive numbers
Because a loan is paid out of your bank account, Excel functions return the payment, interest and principal as negative numbers. By default, these values are highlighted in red and enclosed in parentheses as you can see in the image above.
If you prefer to have all the results as positive numbers, put a minus sign before the PMT, IPMT and PPMT functions.
For the Balance formulas, use subtraction instead of addition like shown in the screenshot below:
Amortization schedule for a variable number of periods
In the above example, we built a loan amortization schedule for the predefined number of payment periods. This quick one-time solution works well for a specific loan or mortgage.
If you are looking to create a reusable amortization schedule with a variable number of periods, you will have to take a more comprehensive approach described below.
1. Input the maximum number of periods
In the Period column, insert the maximum number of payments you are going to allow for any loan, say, from 1 to 360. You can leverage Excel's AutoFill feature to enter a series of numbers faster.
2. Use IF statements in amortization formulas
Because you now have many excessive period numbers, you have to somehow limit the calculations to the actual number of payments for a particular loan. This can be done by wrapping each formula into an IF statement. The logical test of the IF statement checks if the period number in the current row is less than or equal to the total number of payments. If the logical test is TRUE, the corresponding function is calculated; if FALSE, an empty string is returned.
Assuming Period 1 is in row 8, enter the following formulas in the corresponding cells, and then copy them across the entire table.
Payment (B8):
=IF(A8<=$C$3*$C$4, PMT($C$2/$C$4, $C$3*$C$4, $C$5), "")
Interest (C8):
=IF(A8<=$C$3*$C$4, IPMT($C$2/$C$4, A8, $C$3*$C$4, $C$5), "")
Principal (D8):
=IF(A8<=$C$3*$C$4,PPMT($C$2/$C$4, A8, $C$3*$C$4, $C$5), "")
Balance:
For Period 1 (E8), the formula is the same as in the previous example:
=C5+D8
For Period 2 (E9) and all subsequent periods, the formula takes this shape:
=IF(A9<=$C$3*$C$4, E8+D9, "")
As the result, you have a correctly calculated amortization schedule and a bunch of empty rows with the period numbers after the loan is paid off.
3. Hide extra periods numbers
If you can live with a bunch of superfluous period numbers displayed after the last payment, you can consider the work done and skip this step. If you strive for perfection, then hide all unused periods by making a conditional formatting rule that sets the font color to white for any rows after the last payment is made.
For this, select all the data rows if your amortization table (A8:E367 in our case) and click Home tab > Conditional formatting > New Rule… > Use a formula to determine which cells to format.
In the corresponding box, enter the below formula that checks if the period number in column A is greater than the total number of payments:
=$A8>$C$3*$C$4
Important note! For the conditional formatting formula to work correctly, be sure to use absolute cell references for the Loan term and Payments per year cells that you multiply ($C$3*$C$4). The product is compared with the Period 1 cell, for which you use a mixed cell reference - absolute column and relative row ($A8).
After that, click the Format… button and pick the white font color. Done!
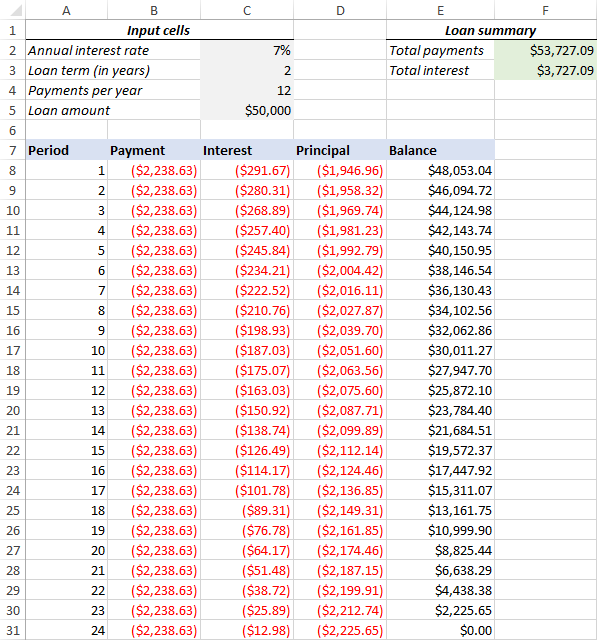
4. Make a loan summary
To view the summary information about your loan at a glance, add a couple more formulas at the top of your amortization schedule.
Total payments (F2):
=-SUM(B8:B367)
Total interest (F3):
=-SUM(C8:C367)
If you have payments as positive numbers, remove the minus sign from the above formulas.
That's it! Our loan amortization schedule is completed and good to go!
How to make a loan amortization schedule with extra payments in Excel
The amortization schedules discussed in the previous examples are easy to create and follow (hopefully :). However, they leave out a useful feature that many loan payers are interested in - additional payments to pay off a loan faster. In this example, we will look at how to create a loan amortization schedule with extra payments.
1. Define input cells
As usual, begin with setting up the input cells. In this case, let's name these cells like written below to make our formulas easier to read:
- InterestRate - C2 (annual interest rate)
- LoanTerm - C3 (loan term in years)
- PaymentsPerYear - C4 (number of payments per year)
- LoanAmount - C5 (total loan amount)
- ExtraPayment - C6 (extra payment per period)
2. Calculate a scheduled payment
Apart from the input cells, one more predefined cell is required for our further calculations - the scheduled payment amount, i.e. the amount to be paid on a loan if no extra payments are made. This amount is calculated with the following formula:
=IFERROR(-PMT(InterestRate/PaymentsPerYear, LoanTerm*PaymentsPerYear, LoanAmount), "")
Please pay attention that we put a minus sign before the PMT function to have the result as a positive number. To prevent errors in case some of the input cells are empty, we enclose the PMT formula within the IFERROR function.
Enter this formula in some cell (G2 in our case) and name that cell ScheduledPayment.
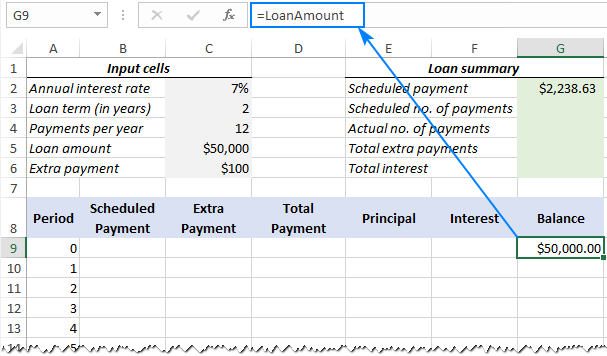
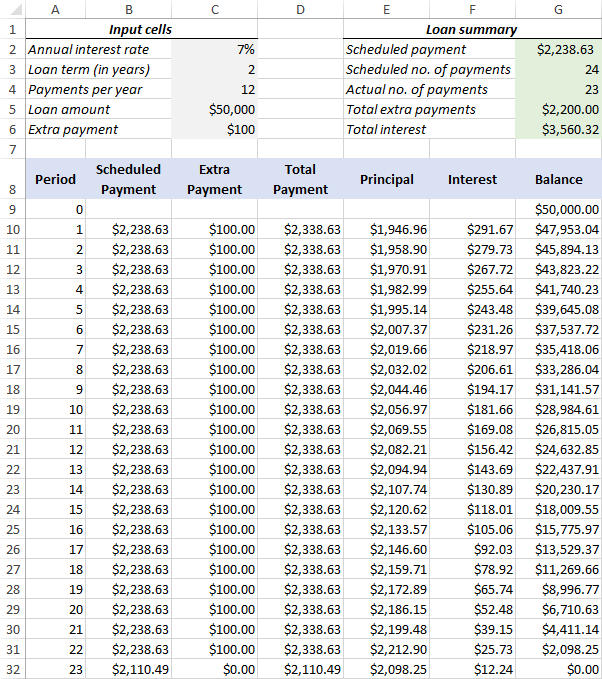
3. Set up the amortization table
Create a loan amortization table with the headers shown in the screenshot below. In the Period column enter a series of numbers beginning with zero (you can hide the Period 0 row later if needed).
If you aim to create a reusable amortization schedule, enter the maximum possible number of payment periods (0 to 360 in this example).
For Period 0 (row 9 in our case), pull the Balance value, which is equal to the original loan amount. All other cells in this row will remain empty:
Formula in G9:
=LoanAmount
4. Build formulas for amortization schedule with extra payments
This is a key part of our work. Because Excel's built-in functions do not provide for additional payments, we will have to do all the math on our own.
Note. In this example, Period 0 is in row 9 and Period 1 is in row 10. If your amortization table begins in a different row, please be sure to adjust the cell references accordingly.
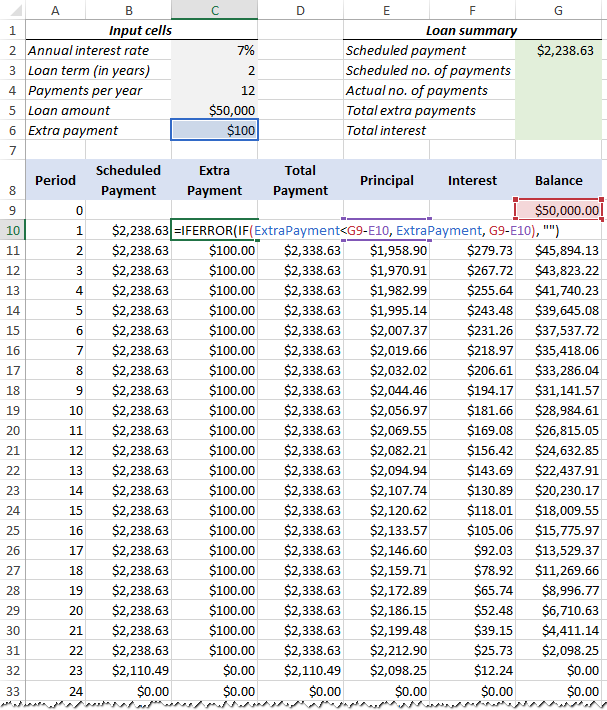
Enter the following formulas in row 10 (Period 1), and then copy them down for all of the remaining periods.
Scheduled Payment (B10):
If the ScheduledPayment amount (named cell G2) is less than or equal to the remaining balance (G9), use the scheduled payment. Otherwise, add the remaining balance and the interest for the previous month.
=IFERROR(IF(ScheduledPayment<=G9, ScheduledPayment, G9+G9*InterestRate/PaymentsPerYear), "")
As an extra precaution, we wrap this and all subsequent formulas in the IFERROR function. This will prevent a bunch of various errors if some of the input cells are empty or contain invalid values.
Extra Payment (C10):
Use an IF formula with the following logic:
If the ExtraPayment amount (named cell C6) is less than the difference between the remaining balance and this period's principal (G9-E10), return ExtraPayment; otherwise use the difference.
=IFERROR(IF(ExtraPayment<G9-E10, ExtraPayment, G9-E10), "")
Tip. If you have variable additional payments, just type the individual amounts directly in the Extra Payment column.
Total Payment (D10)
Simply, add the scheduled payment (B10) and the extra payment (C10) for the current period:
=IFERROR(B10+C10, "")
Principal (E10)
If the schedule payment for a given period is greater than zero, return a smaller of the two values: scheduled payment minus interest (B10-F10) or the remaining balance (G9); otherwise return zero.
=IFERROR(IF(B10>0, MIN(B10-F10, G9), 0), "")
Please note that the principal only includes the part of the scheduled payment (not the extra payment!) that goes toward the loan principal.
Interest (F10)
If the schedule payment for a given period is greater than zero, divide the annual interest rate (named cell C2) by the number of payments per year (named cell C4) and multiply the result by the balance remaining after the previous period; otherwise, return 0.
=IFERROR(IF(B10>0, InterestRate/PaymentsPerYear*G9, 0), "")
Balance (G10)
If the remaining balance (G9) is greater than zero, subtract the principal portion of the payment (E10) and the extra payment (C10) from the balance remaining after the previous period (G9); otherwise return 0.
=IFERROR(IF(G9 >0, G9-E10-C10, 0), "")
Note. Because some of the formulas cross reference each other (not circular reference!), they may display wrong results in the process. So, please do not start troubleshooting until you enter the very last formula in your amortization table.
If all done correctly, your loan amortization schedule at this point should look something like this:
5. Hide extra periods
Set up a conditional formatting rule to hide the values in unused periods as explained in this tip. The difference is that this time we apply the white font color to the rows in which Total Payment (column D) and Balance (column G) are equal to zero or empty:
=AND(OR($D9=0, $D9=""), OR($G9=0, $G9=""))
Voilà, all rows with zero values are hidden from view:
6. Make a loan summary
As a finishing touch of perfection, you can output the most important information about a loan by using these formulas:
Scheduled number of payments:
Multiply the number of years by the number of payments per year:
=LoanTerm*PaymentsPerYear
Actual number of payments:
Count cells in the Total Payment column that are greater than zero, beginning with Period 1:
=COUNTIF(D10:D369,">"&0)
Total extra payments:
Add up cells in the Extra Payment column, beginning with Period 1:
=SUM(C10:C369)
Total interest:
Add up cells in the Interest column, beginning with Period 1:
=SUM(F10:F369)
Optionally, hide the Period 0 row, and your loan amortization schedule with additional payments is done! The screenshot below shows the final result:
Amortization schedule Excel template
To make a top-notch loan amortization schedule in no time, make use of Excel's inbuilt templates. Just go to File > New, type "amortization schedule" in the search box and pick the template you like, for example, this one with extra payments:
Then save the newly created workbook as an Excel template and reuse whenever you want.
That's how you create a loan or mortgage amortization schedule in Excel. I thank you for reading and hope to see you on our blog next week!
Available downloads
Amortization Schedule examples (.xlsx file)
88 comments
Good day.
Thank you for this. I am looking to add a column for periodic withdrawls for repairs. Anybody can help here. Want to see how it affects the timeline. Tx Jacqui
Or maybe you have it correct, but it is just very hard to see because of the impossibly short amortization period? I will try this with a 30-year am and it will be clearer to see.
Just one thing that may help some people who are saying there that they cannot get this to work. I think it is the backwards phrasing. Instead of saying "put $25,000 in cell b4," it is easier for the human brain to process so many steps if they are all put in the order that the eye/brain move:
1. Go to cell B4.
2. Enter the original loan balance of $25,000.
I have found this backward phrasing so frustrating that I am going to exit this page and write my own formulas.
I'm confused. The point of amortization is for the lender to front load his receipt of interest. To do this, the bulk of the early payments to go interest, and a tiny part goes toward principal paydown. This ratio reverses as you move through the months/years of payments.
Doesn't your chart show the opposite? (With the bulk of the early payments going toward principal, which is wrong in USA lending.)
I just saw that you figured it out yourself in your later comment.
You're overthinking things. The reason the early principal in this example is a lot more than the interest is because the term the 50,000 loan is being paid in is very short compared to the size of the loan. Change the loan amount to be paid for a longer period of time and the principal changes accordingly. The interest caculation is accurate.
Hi. Trying to modify this table to account for additional monthly charges.
which adds to the loan amount instead of extra payments which reduces the loan amount. Do I simply add a minus sign to the extra payment figures or is there another way I can do this? Considering the interest rate is on the amount borrowed and not the total repayment amount. Thanks.
thnks!
Thank you Svetlana Cheusheva! I followed your examples and they worked perfectly. I did have to look up the defined naming, but other than that, you provided everything.
I followed your tutorial using the same example data and got the exact same results (and learnt a lot along the way, thanks!), which is great. However, I also followed a different tutorial (not from ablebits), which used PPMT, IPMT and included extra payments. The results were similar, but the Total Interest ended up being $166.77 higher than in your example.
The logic used in both tutorials seems the same, ie balance-principal-extra payment, and both assume the extra payment go towards the Principle Balance, but the results are different. I'm guessing it's as you said in this post, "Because Excel's built-in functions do not provide for additional payments, we will have to do all the math on our own", but I'd love to understand why the difference.
Your formula to calculate the balance is: =IFERROR(IF(G9 >0, G9-E10-C10, 0), "")
The other tutorial's formula is: =I10-K10-N10 (which is essentially the same as 'G9-E10-C10' ). So, it seems the difference is in how the input cells are calculated:
I10 = Starting Balance
K10 = Principal PMT Portion (cell formula is -PPMT(InterestRate/12, Period, Term, Principle (absolute reference)))
N10 = Extra Payment
Can you shed any light?
I need assistance in setting up a loan amortization schedule with the following columns:
1. Due date ( due dates should be one month apart starting from the loan issue date)
2. Payment date
3. Payment amount
4. Accrued interest
5. Principal payment
6. Interest Payment
7. Principal balance
8. Interest balance
The rules for the schedule are as follows:
1. The loans are amortized loans; interest is charged on the reducing balance of the principal
2. If a client misses payment on a due date, interest is charged on principal plus total interest accrued as at the last due date.
3. Repayment is first setoff against any interest accrued and the remainder, if any, if used to reduce the principal outstanding.
Thank you.
Your request goes beyond the advice we provide on this blog. This is a complex solution that cannot be found with a single formula. If you have a specific question about the operation of a function or formula, I will try to answer it.
I'm trying to create the schedule with extra payments but can't get past steps 1 and 2...
Are we supposed to name the input cells as "InterestRate - C2 (annual interest rate)" or "annual interest rate" in cell A2?
Also, the instruction for step 1 looks like were supposed to type "InterestRate" as a hyperlink somehow in cell D2 but in the example for step 2, that cell is blank.
I have tried the names each way and can't get the balance or schedule payment fields to calculate.
Nevermind... I didn't know about the "Name Box". Now that I know about that, this instruction just got much easier!
Thank you!
QUESTION. NOT THAT I AM EXCEL EXPERT, I BUILT TABLE ABOVE. DON'T UNDERSTAND HOW INTEREST IS CALCULATED WHEN THE BALANCE IS NOT IN THE FORMULA. I TESTED FORMULA BY ADDING 200.00 TO PAYMENT AMOUNT, BALANCE WAS REDUCED, BUT INTEREST IN ALL COLUMNS REMAINED UNCHANGED.
Hi Team, these are really nice schedules. However, could you please assist with a schedule that has additional borrowings plus the initial loan.
Initial loan in year 1 and subsequent loans in years 3,4 and 5 respectively.
Thank you Team
Hello!
I am looking for a sheet like this but can hold 30+ vehicles on one sheet and goes vertical with the information and not horizontal. Do you know of anything out there like that?
Hello!
You can change data from vertical to horizontal using the TRANSPOSE function. Here is the article that may be helpful to you: TRANSPOSE function in Excel to change column to row with formula.
I need to add an extra detail of moratorium along with the extra payment feature in the provided sample file. If the file is already provided or created, can you share the same?
Dear Sir
Can be available Loan Amortization table in excel
Can it be possible client wise auto update loan amortization table?
Also if possible interest rate change so auto update automatic in excel
Extra Payments means (Start at Payment No,Extra Payment,Payment Interval,Extra Annual Payment,Payment,Total Extra Payments) Additional Payment ,Variable or Fixed Rate ,Impact of interest rate HIKE on your loan EMI & repayment schedule & Impact of interest rate CUT on your loan EMI & repayment schedule ? how to create in excel & Suppose provide only interest
Why would the payments not be at the beginning of the period (using type 1 in the excel PMT calculation)? It wouldn’t make sense to make monthly mortgage payments at the end of the month.
Real Estate payments are made in arrears so end of period is appropriate for real estate loans.
How to add extra payments on non payment due dates?
Is there a way to keep the Annual Interest Rate cell from rounding up? My actual annual interest rate is 19.6% and when I enter it into the cell, the number is automatically rounded up to 20%, which causes the running balance to be slightly off. I am not very experienced with excel and have probably done something incorrectly. I appreciate your help and information.
Hello!
Here is the article that may be helpful to you: Precision of Excel calculations. Change the cell number format and increase the number of decimal places.
I hope it’ll be helpful.
To the author, great table!. I was looking for something like this. I would like to change something on it though and not to sure of the process. I notice when filling in the loan term the cells automatically populate which is brilliant! However, when putting in 25 or 30 years the max cells that populate end at cell 369. How would I change that to match 25 years? I've tried auto filling the other cells but they stay blank.
This is a great tool. My target is to dynamically revisit my current Mortgage Balance with large payments (e.g., $100,000.00 at a time to see what the imapcaat would be on the payment. The concept is to pay the current Mortgage amount offr Early.
Thanks....
Jim Kerr, Sr.
Hi,
Good day. Thanks for the wonderful amortization tool and the steps tutorial.
Have you done one with a principle moratorium option? Will appreciate receiving a copy of the same via mail.
Thanks.
Bosco
Thank you for the tutorial on making an Amortization Schedule. I learned a few things from you as well.