Essentially, this tutorial gives answers to three "what" questions. What is present value of annuity? What is the present value formula? What discount or interest rate to use for present value calculation?
If offered a choice to receive a certain sum of money right now or defer the payment into the future, which would you choose? For most people, taking money now is a natural instinct. In the financial world, this is explained by the time value of money concept.
There are two main terms that measure how much the value of money changes over time: future value (FV) and present value (PV). If you are curious to know the worth of your investment after a certain period, calculate its future value as explained in the FV function tutorial. If you wish to find the current worth of money, then you need to calculate present value, and this tutorial shows how to quickly do this in Excel.
Present value of annuity
When putting deposits to a saving account, paying home mortgage and the like, you usually make the same payments at regular intervals, e.g. weekly, monthly, quarterly, or yearly. Such series of payments (either inflow or outflow) made at equal intervals is called an annuity.
The present value of annuity can be defined as the current value of a series of future cash flows, given a specific discount rate, or rate of return. For this reason, present value is sometimes called present discounted value. The bigger the discount rate, the smaller the present value.
The concept of present value (PV) is based on the idea of the time value of money. In essence, any amount you have now is worth more than the same amount in the future due to its capacity to potentially earn interest. The sooner a certain sum is received, the more it is worth. In simple words, this financial concept is described by the old saying: "A dollar today is worth more than a dollar tomorrow".
In financial analysis, present value is highly important. It lets you clearly understand how much money you need to invest today to reach the target amount in the future. Also, it can help you make an informed decision on whether to accept a specific cash rebate, evaluate projects in the capital budgeting, and more.
In everyday life, the present value comes in useful too. For example, it can help you determine which is more profitable - to take a lump sum right now or receive an annuity over a number of years.
Present value formula
When talking about a single cash flow, i.e. one payment period, the present value formula is as simple as this:

Where:
- FV - future value
- r - discount or interest rate
Suppose you want to have $11,000 in your saving account one year from now. How much should you deposit today provided that your bank offers an annual interest rate of 10%?
To find the present value of this investment, do this math:
![]()
For a series of cash flows, the present value formula is slightly more complicated:

Where:
- r – discount or interest rate
- n – the number of time periods
- i – the cash flow period
For example, to find the present value of a series of three $100 payments made at equal intervals and discounted at 10%, you can perform these calculations:
![]()
How to calculate present value in Excel - formula examples
The previous section shows how to calculate the present value of annuity manually. The good news is that Microsoft Excel has a special PV function that does all calculations in the background and outputs the final result in a cell.
If you are not familiar with this function, it's a good idea to begin with the above linked tutorial that explains the syntax.
Present value formula for a single payment
Suppose you have won a cash prize in a lottery and have two options - to get $10,000 right now or $11,000 in a year. Which is a better deal?
To get your answer, you need to calculate the present value of the amount you will receive in the future ($11,000). For this, you need to know the interest rate that would apply if you invested that money today, let's assume it's 7%.
With the above information in mind, set up your worksheet as follows:
- Annual interest rate (C2): 7%
- No. of years (C3): 1
- Future value (C4): 11,000
The formula to calculate the present value of the investment is:
=PV(C2, C3, ,C4)
Please pay attention that the 3rd argument intended for a periodic payment (pmt) is omitted because our PV calculation only includes the future value (fv), which is the 4th argument.
Also, please note that the returned present value is negative, since it represents a presumed investment, which is an outflow. In other words, if you invested $10,280 at 7% now, you would get $11,000 in a year.

Getting back to the initial question - receiving $11,000 one year from now is a better choice, as its present value ($10,280) is greater than the amount you are offered right now ($10,000).
In the above example, an interest rate is compounded yearly. However, most savings accounts pay monthly compound interest. Will it impact the calculation? Let's see…
Because the interest is compounded 12 times a year, we divide 7% by 12 to get the correct periodic rate, and multiply 1 by 12 to have the right nper:
=PV(C2/12, C3*12, ,C4)
As you can see below, with an interest rate compounded monthly, the present value is much smaller, which totally changes the answer to the original question :)
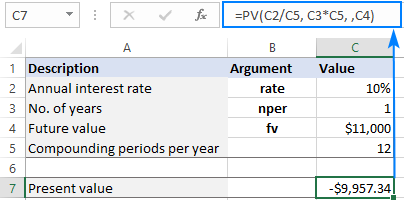
Note. These examples assume ordinary annuity when all the payments are made at the end of a period. For annuity due, please see this example.
Present value formula for annuity
When calculating the present value of annuity, i.e. a series of even cash flows, the key point is to be consistent with rate and nper supplied to a PV formula.
To get a correct periodic interest rate (rate), divide an annual interest rate by the number of compounding periods per year:
- Monthly: rate = annual interest rate / 12
- Quarterly: rate = annual interest rate / 4
- Semiannual: rate = annual interest rate / 2
To get the total number of periods (nper), multiply the length of an annuity in years by the number of periods per year:
- Monthly: nper = no. of years * 12
- Quarterly: nper = no. of years * 4
- Semiannual: nper = no. of years * 2
For this example, we will be using a series of $100 payments that we calculated manually in the first part of this tutorial and input the following data in a worksheet:
- Annual interest rate (B2): 10%
- No. of years (B3): 3
- Annual payment (B4): -100
Please notice that the payment is expressed by a negative number because it's an outflow.
Assuming the payments are made at the end of each year, you can calculate the present value with this formula:
=PV(B2, B3, B4)
As shown in the image below, the PV formula returns the same result as the manual calculation - $248.69.

If the payments are made monthly, then add one more input cell (B5) for the number of periods per year (12 on our case). To get the correct present value, convert an annual interest rate to a monthly rate (B2/B5) and provide the total number of periods for annuity (B3*B5):
=PV(B2/B5, B3*B5, B4)

Present value formula for different annuity types
The annuity type is controlled by the 5th (optional) argument of the PV function, named type:
- For ordinary (regular) annuity, where all payments are made at the end of a period, use 0 for type. This is the default value that applies automatically when the argument is omitted.
- For annuity due, where all payments are made at the end of a period, use 1 for type.
To see the effect of different annuity types, set up your spreadsheet like shown below and enter your data in the corresponding cells:
- Annual interest rate: B2
- No. of years: B3
- Payment amount: B4
- Annuity type: B5
- Periods per year: B6
For regular annuity, type 0 in B5; for annuity due, type 1. To prevent mistakes, it makes sense to create a drop-down list for B5 that only allows 0 and 1 values.
To calculate the present value of a series of payments, we will be using the below formula. Please pay attention that the 4th argument (fv) is omitted because the future value is not included in the calculation.
=PV(B2/B6, B3*B6, B4, ,B5)
As shown in the screenshot below, the annuity type does make the difference. With the same term, interest rate and payment amount, the present value for annuity due is higher.

How to create present value calculator in Excel
Knowing how to write a PV formula for a specific case, it's quite easy to tweak it to handle all possible cases. Simply provide input cells for all the arguments of the PV function. If some argument is not used in a particular calculation, the user will leave that cell blank.
In our case, we organize the data as follows:
- Annual interest rate: B2
- Annuity term in years: B3
- Payment amount: B4
- Future value: B5
- Annuity type: B6
- Periods per year: B7
The present value calculator formula in B9 is:
=PV(B2/B7, B3*B7, B4, B5, B6)
Assuming you make a series of $500 payments at the beginning of each quarter for 3 years with a 7% annual interest rate, set up the source data as shown in the image below. And the present value calculator will output the result:
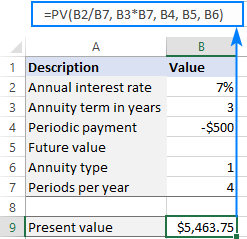
For the PV calculator to work correctly, please follow these usage notes:
- For a lump sum investment that will pay a certain amount in the future, define the future value (B5). For an annuity spread out over a number of years, specify the periodic payment (B4).
- Any money that you pay out should be represented by a negative number; any money that you receive - by a positive number.
- The Periods per year cell (B7) must not be blank or 0 because this will cause a #DIV/0 error. In case of annual cash flows, enter 1 in that cell.
I hope our examples have shed some light on how to how to calculate present value of annuity in Excel. Thank you for reading and hope to see you on our blog next week!
Practice workbook for download
Present value formula in Excel (.xlsx file)
 by
by