Mean, median and mode in Excel

When analyzing numerical data, you may often be looking for some way to get the "typical" value. For this purpose, you can use the so-called measures of central tendency that represent a single value identifying the central position within a data set or, more technically, the middle or center in a statistical distribution. Sometimes, they are also classified as summary statistics.

The three main measures of central tendency are Mean, Median and Mode. They all are valid measures of central location, but each gives a different indication of a typical value, and under different circumstances some measures are more appropriate to use than others.

How to calculate mean in Excel

Arithmetic mean, also referred to as average, is probably the measure you are most familiar with. The mean is calculated by adding up a group of numbers and then dividing the sum by the count of those numbers.

For example, to calculate the mean of numbers {1, 2, 2, 3, 4, 6}, you add them up, and then divide the sum by 6, which yields 3: (1+2+2+3+4+6)/6=3.

In Microsoft Excel, the mean can be calculated by using one of the following functions:

  • AVERAGE- returns an average of numbers.
  • AVERAGEA - returns an average of cells with any data (numbers, Boolean and text values).
  • AVERAGEIF - finds an average of numbers based on a single criterion.
  • AVERAGEIFS - finds an average of numbers based on multiple criteria.

For the in-depth tutorials, please follow the above links. To get a conceptual idea of how these functions work, consider the following example.

In a sales report (please see the screenshot below), supposing you want to get the average of values in cells C2:C8. For this, use this simple formula:

=AVERAGE(C2:C8)

To get the average of only "Banana" sales, use an AVERAGEIF formula:

=AVERAGEIF(A2:A8, "Banana", C2:C8)

To calculate the mean based on 2 conditions, say, the average of "Banana" sales with the status "Delivered", use AVERAGEIFS:

=AVERAGEIFS(C2:C8,A2:A8, "Banana", B2:B8, "Delivered")

You can also enter your conditions in separate cells, and reference those cells in your formulas, like this:
Calculating the arithmetic mean in Excel

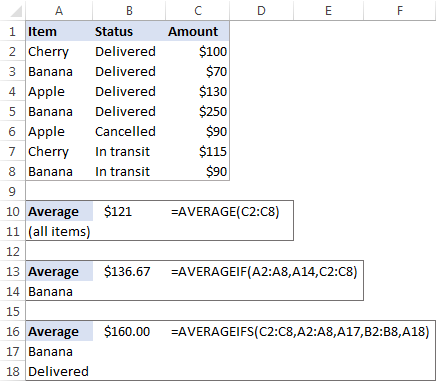
How to find median in Excel

Median is the middle value in a group of numbers, which are arranged in ascending or descending order, i.e. half the numbers are greater than the median and half the numbers are less than the median. For example, the median of the data set {1, 2, 2, 3, 4, 6, 9} is 3.
Calculating the median for the data set with an odd number of values

This works fine when there are an odd number of values in the group. But what if you have an even number of values? In this case, the median is the arithmetic mean (average) of the two middle values. For example, the median of {1, 2, 2, 3, 4, 6} is 2.5. To calculate it, you take the 3rd and 4th values in the data set and average them to get a median of 2.5.
Calculating the median for the data set with an even number of values

In Microsoft Excel, a median is calculated by using the MEDIAN function. For example, to get the median of all amounts in our sales report, use this formula:

=MEDIAN(C2:C8)

To make the example more illustrative, I've sorted the numbers in column C in ascending order (though it is not actually required for the Excel Median formula to work):
Calculating median in Excel

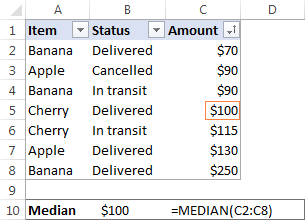
In contrast to average, Microsoft Excel does not provide any special function to calculate median with one or more conditions. However, you can "emulate" the functionality of MEDIANIF and MEDIANIFS by using a combination of two or more functions like shown in these examples:

How to calculate mode in Excel

Mode is the most frequently occurring value in the dataset. While the mean and median require some calculations, a mode value can be found simply by counting the number of times each value occurs.

For example, the mode of the set of values {1, 2, 2, 3, 4, 6} is 2. In Microsoft Excel, you can calculate a mode by using the function of the same name, the MODE function. For our sample data set, the formula goes as follows:

=MODE(C2:C8)
Calculating mode in Excel

In situations when there are two or more modes in your data set, the Excel MODE function will return the lowest mode.

Mean vs. median: which is better?

Generally, there is no "best" measure of central tendency. Which measure to use mostly depends on the type of data you are working with as well as your understanding of the "typical value" you are attempting to estimate.

For a symmetrical distribution (in which values occur at regular frequencies), the mean, median and mode are the same. For a skewed distribution (where there are a small number of extremely high or low values), the three measures of central tendency may be different.

Since the mean is greatly affected by skewed data and outliers (non-typical values that are significantly different from the rest of the data), median is the preferred measure of central tendency for an asymmetrical distribution.

For instance, it is generally accepted that the median is better than the mean for calculating a typical salary. Why? The best way to understand this would be from an example. Please have a look at a few sample salaries for common jobs:

  • Electrician - $20/hour
  • Nurse - $26/hour
  • Police officer - $47/hour
  • Sales manager - $54/hour
  • Manufacturing engineer - $63/hour

Now, let's calculate the average (mean): add up the above numbers and divide by 5: (20+26+47+54+63)/5=42. So, the average wage is $42/hour. The median wage is $47/hour, and it is the police officer who earns it (1/2 wages are lower, and 1/2 are higher). Well, in this particular case the mean and median give similar numbers.

But let's see what happens if we extend the list of wages by including a celebrity who earns, say, about $30 million/year, which is roughly $14,500/hour. Now, the average wage becomes $2,451.67/hour, a wage that no one earns! By contrast, the median is not significantly changed by this one outlier, it is $50.50/hour.
Mean vs. median for calculating typical salary

Agree, the median gives a better idea of what people typically earn because it is not so strongly affected by abnormal salaries.

This is how you calculate mean, median and mode in Excel. I thank you for reading and hope to see you on our blog next week!

Table of contents

36 comments

  1. Good day

    I am looking for an Excel template where I can input marks for a subject and adjust it upwards or downward with a scale factor to pull it in line with historical data. I.e., if cohort learners consistently received a 70% average in a subject but suddenly there is a massive drop in exam due to question papers not being valued, I want to adjust the marks upwards by a fair scale factor to bring marks in line for the year and histrical data. Where can I find such an Excel template?

  2. Using Excel from the Office 365 suite of applications, in English, a police officer needs to divide the sum of the range of cells from A3 to A6 by the average of the range of cells from B3 to B6. In the cell that will receive the result, you must use the formula:
    A) =SUM (A3;A6) /MEAN (B3;B6)
    B) =SUM (A3,A6) /MEAN(B3,B6)
    C) =SUM (A3:A6) /MEAN (B3:B6)
    D) =SUM (A3..A6) /MEAN (B3..B6)
    E) =SUM (A3+A4+A5+A6) /MEAN (B3+B4+B5+B6)

    A) =SUM (A3;A6) /AVERAGE (B3;B6)
    B) =SUM (A3,A6) /AVERAGE (B3,B6)
    C) =SUM (A3:A6) /AVERAGE (B3:B6)
    D) =SUM (A3..A6) /AVERAGE (B3..B6)
    E) =SUM (A3+A4+A5+A6) /AVERAGE (B3+B4+B5+B6)

    is it correct to say that both the letter "c" and also the letter "d" get the same results?

    Can you help me with this?

    1. The MEAN function is not available in the English version of Excel. As I said, you can check the results of these formulas yourself in your Excel.

  3. Can you divide the mean of cells G15:G20 by the median of cells M13:N13

    Kind regards...

  4. How to compute mean, median, mode, standard deviation, variance in Microsoft Excel using functions

  5. Is it possible to send your lessons to my email id regularly?

    You may kindly reply to my mail ID.

    Thanks.

  6. Hello Sir,
    I have a list of Income amounts and i want to eliminate as "Higher Income" ,"Medium Income" and "Lower Income" in a seprate column using one formula kindly help me.

  7. Hello,
    I am wanting to convert 3 datasets into 1. I have graphed the 3 datasets (curves), but I am struggling to have an accurate (1) curve, that is composed by all 3, by using =AVERAGE.

  8. Thanks

  9. Is it possible to calculate mean, mode, median for grouped data in excel. if yes which formulas are applicable for each of the categories provided

  10. How do calculate the mean if my data is given in decimals, using excel ?

  11. Thanks a lot for this amazing and concise microsoft excel tutorial on mean median and mode. I am an Excel data analyst, but I must confess that I learnt something new from this article. Am the CEO of microsofttut blog.

  12. Thank you so much.
    God bless.
    Ellen

  13. I noticed when trying to calculate mode in one of my spreadsheets that after inputting new data points the mode value wasn't updating. Upon further investigation I realize that Excel is limited to 255 datapoints whereas I am trying to utilize over 1000. What alternatives or workarounds are there to this limitation?

  14. Hi there
    I would like to know how to find the mode using the frequency distribution table using Excel. The frequency table has numerical scores in first column and the frequencies in the second column.
    Thanking you
    Dhiren Prasad

  15. Question 4,
    What is an MS EXCEL when the fifth root of the in the F3 subtracted from the median of the median of the median of the scores in cells 4?6.
    J2:K3

  16. Question 3
    What is the MS EXCEL formula when, given the Variance in cell d1, find the standard deviation raised to the power of the number of values in cell A3:A5

  17. Next question, what is the MS EXCEL formula to find the principal, given the annual interest rate in cell G5, the year of investment in cell G6 and the final value in G8. The interest here is compounded every 3 months.
    Your inputs would be much appreciated.

  18. Hello, my name is Gibs Jeremiah. Could you please provide me a example of this question. What is an MS EXCEL formula when mode of the values in cell C6:C12, divided by the mean of values in cells L4:K6 and 100. The result is then raised to the power of 3.
    Your inputs would be much appreciated.

    1. Hi Gibs,
      Here's the formula as per your conditions:
      =(MODE(C6:C12)/AVERAGE(K4:L6)/100)^3

  19. ms excel formula for the mode of values in cells c6:c12, devide by the mean of values in cells l4:k6 and 100, result is then raised to the power of 3

  20. How to find median from group data with the help of excel2016

    1. Manab:
      Where the numbers are in cells E64 through E70
      =MEDIAN(E64:E70) put this in an empty cell of your choice.

Post a comment



Thank you for your comment!
When posting a question, please be very clear and concise. This will help us provide a quick and relevant solution to
your query. We cannot guarantee that we will answer every question, but we'll do our best :)