by The tutorial demonstrates two easy ways to calculate weighted average in Excel - by using the SUM or SUMPRODUCT function.
In one of the previous articles, we discussed three essential functions for calculating average in Excel, which are very straightforward and easy-to-use. But what if some of the values have more "weight" than others and consequently contribute more to the final average? In such situations, you'll need to calculate the weighted average.
Although Microsoft Excel doesn't provide a special weighted average function, it does have a couple of other functions that will prove useful in your calculations, as demonstrated in the formula examples that follow.
What is weighted average?
Weighted average is a kind of arithmetic mean in which some elements of the data set carry more importance than others. In other words, each value to be averaged is assigned a certain weight.
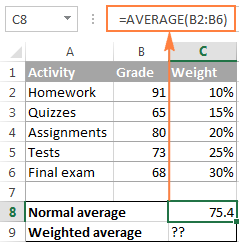
Students' grades are often calculated using a weighted average, as shown in the following screenshot. A usual average is easily calculated with the Excel AVERAGE function. However, we want the average formula to consider the weight of each activity listed in column C.
In mathematics and statistics, you calculate weighted average by multiplying each value in the set by its weight, then you add up the products and divide the products' sum by the sum of all weights.
In this example, in order to calculate the weighted average (overall grade), you multiply each grade by the corresponding percentage (converted to a decimal), add up the 5 products together, and divide that number by the sum of 5 weights:
((91*0.1)+(65*0.15)+(80*0.2)+(73*0.25)+(68*0.3)) / (0.1+0.15+0.2+0.25+0.3)=73.5
As you see, a normal average grade (75.4) and weighted average (73.5) are different values.
Calculating weighted average in Excel
In Microsoft Excel, weighted average is calculated using the same approach but with far less effort because Excel functions will do most of the work for you.
Calculating weighted average using SUM function
If you have basic knowledge of the Excel SUM function, the below formula will hardly require any explanation:
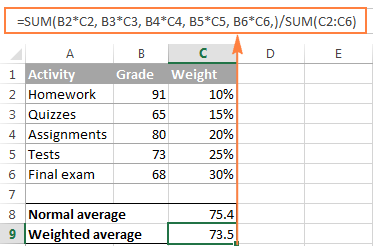
=SUM(B2*C2, B3*C3, B4*C4, B5*C5, B6*C6,)/SUM(C2:C6)
In essence, it performs the same calculation as described above, except that you supply cell references instead of numbers.
As you can see in the screenshot, the formula returns exactly the same result as the calculation we did a moment ago. Notice the difference between the normal average returned by the AVERAGE function (C8) and weighted average (C9).
Although the SUM formula is very straightforward and easy to understand, it is not a viable option if you have a large number of elements to average. In this case, you'd better utilize the SUMPRODUCT function as demonstrated in the next example.
Finding weighted average with SUMPRODUCT
Excel's SUMPRODUCT function fits perfectly for this task since it is designed to sum products, which is exactly what we need. So, instead of multiplying each value by its weight individually, you supply two arrays in the SUMPRODUCT formula (in this context, an array is a continuous range of cells), and then divide the result by the sum of weights:
Supposing that the values to average are in cells B2:B6 and weights in cells C2:C6, our Sumproduct Weighted Average formula takes the following shape:
=SUMPRODUCT(B2:B6, C2:C6) / SUM(C2:C6)
To see the actual values behind an array, select it in the formula bar and press the F9 key. The result will be similar to this:
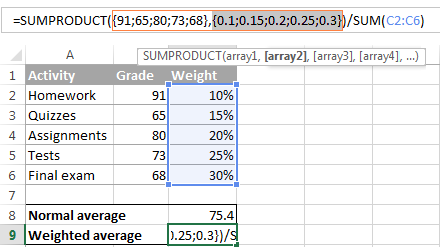
So, what the SUMPRODUCT function does is multiply the 1st value in array1 by the 1st value in array2 (91*0.1 in this example), then multiply the 2nd value in array1 by the 2nd value in array2 (65*0.15 in this example), and so on. When all of the multiplications are done, the function adds up the products and returns that sum.
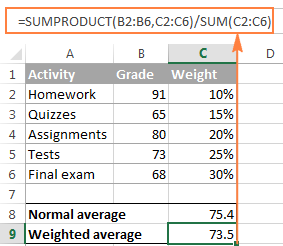
To make sure that the SUMPRODUCT function yields a correct result, compare it to the SUM formula from the previous example and you will see that the numbers are identical.
When using either the SUM or SUMPRODUCT function to find weight average in Excel, weights do not necessarily have to add up to 100%. Nor do they need to be expressed as percentages. For example, you can make up a priority / importance scale and assign a certain number of points to each item, as demonstrated in the following screenshot:
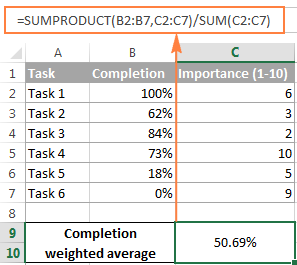
Well, that's all about calculating weighted average in Excel. You can download the sample spreadsheet below and try the formulas on your data. In the next tutorial, we are going to have a close look at calculating moving average. I thank you for reading and look forward to seeing you next week!
Practice workbook
Excel Weighted Average - examples (.xlsx file)
42 comments
Calculating Estimation Average in Multiple Exams
Total exams count-10
But one student written only 8 exams reaming all present how to Calcuating Estimation Average in Excel
Plz let me what is the formula use above condition
I have bond trading data which consists of trade date, trade (buy/sell), bond issue, coupon, traded yield, traded clean price and traded dirty price. I keep adding the transactions as per those columns. I intend to compute the volume-weighted average (VWA) values per trade row. If it is a purchase (get VWA of the yield, clean and dirty for that bond issue). If it is a sale it looks up most recent VWA value for the respective bond issue and assigns/displays it.
More of a trading log with each row computing the VWA values per each entry - yield, clean and dirty. If purchase compute VWA values, if sale, lookup the last VWA values based on the bond issue (cannot sell something that is not there). This column data shall be used compute the profit and loss, per row (mainly upon sale, for purchases it is blank).
I am avoiding CSE array functions. Attempting to use SUMPRODUCT, but it breaks (generates wrong VWA
values) when there are more one purchase entries.
Hi!
I am not an expert in bond trading and therefore cannot guess what you want to calculate.
Explain what you want to calculate, and give an example of the source data and the expected result.
This Blog is helpful.
Hi,
Can u explain me this situation where I have an yearly data for every particular meal dish starting Jan-21 to Dec-21 on a daily level.
Now every dish is available for different no. of days in a week. For eg, Butter chicken will be available for all 7 days of a week but maybe the Turkey sandwich will be available only twice a week.
How do i calculate the daily weighted average for each dish.
Hello!
The formula for calculating the weighted average can be completely different depending on how your data looks. If column B is the quantity and column C is the price, then the formula might be:
=SUMPRODUCT(B2:B53, C2:C53) / SUM(C2:C53)
If this is not what you wanted, please describe the problem in more detail.
Thank you! This is very easy and helpful.
If given a chance to use calculator and Microsoft excel, which one will you choose?
Hi - how does one calculate a weighted average if you only have one data set without a weight column. For instance, I have 6 figures (5 of them are under $102 and one is $1M). The simple average here would be skewed by the $1M. So how would I obtain a more "weighted" average here?
This is the sample data:
$101,
$102,
$91,
$100,
$90,
$1,000,000
Hello!
For non-typical values, it is recommended to calculate not the average, but the median. You can learn more about mean, median and mode in this article.
I hope it’ll be helpful.
Hi,
No need to divide by the percentage as it is always like dividing by 1.
SUMPRODUCT(values_range, weights_range) is enough.
Don't think so - you don't get the same result
That's correct your weights should add to 1 so no need to divide by 1. I mean you can but there's no point.
Op Or
666.29 -10.79
734.57 9.45
800.39 41.7
2201.25 40.36
Weighted Average=?
HELP!!!!
How do I calculate the weighted average?
Month= 1-12
Amount= 159K; 67K; 92K; 83K; 125K; 119K; 213K; 85K; 79K; 113K; 124K; 183K
Hello Lynn!
I hope you have studied the recommendations in the above tutorial. Please let me know in more detail what formula you used and what problem or error occurred. In that case I will try to help you.
I will be holding a random drawing for 80 people. Each person will have a number of raffle tickets earned before the drawing. I'd like to assign a weight to the people who have more raffle tickets than people who have less. Example: Person A has 10 raffle tickets and Person B has 3 raffle tickets, I'd like to assign a specific percentage for Person A and Person B. Person A probability should be higher than Person B. Is there a way I can do this and then hold a random drawing?
if
Cutoff = 60 Marks
Max Score = 70 Marks
Weightage = 20%
how to calculate score ( Weightage) if any body have 65 Marks
Thank you, I found the tutorial very useful!
I want to perform all the calculations in one cel,item,Quantity and Moisture weighted average in exal
How do I get the weighted aver per FY (total?
FY16 FY17 FY18
$4,600 $3,618 $53
($58) ($9) ($460)
$140 $463 $99
$6,627 $6,101 $6,420
$0 $0 ($694)
($8) ($2,303) $0
($4,501) ($6,079) ($1,902)
$6,800 $1,791 $3,516
How would i add a new number to a cell and give me an average of the amount of entries
first entry 46
a week later i want to add 52 to the same cell
a week later i want to add 58 to the same cell
I want the results to be 52 printed in the cell
156 / 3 = 52
Hello, Gerald.
If you want to perform all the calculations in one cell, you'll have to manually update its content each time. If, however, your task if to find average value of multiple cells, please have a look at the following article on our blog:
How to calculate average (mean) in Excel - AVERAGE, AVERAGEIF, AVERAGEIFS formula examples
Hope you'll find this information helpful.
So a bit more complex of a weighing that I need and I have struggled with it for a while.
I basically have two separated weighted categories which each have 3 internal weighted categories but everything combines for one single score. I could not get the sum product function to align with the answer that populates from our automatic dashboard system .
Example:
Total percentage of score is 100% broken into two main categories at 70 and 30 percent
Category 1: 70% weight
Sub Category 1 weight: 40% of the total 70%
Sub Category 2 weight: 35% of the total 70%
Sub Category 3 weight: 25% of the total 70%
Category 2: 30% weight
Sub Category 1: 33.3% of the total 30%
Sub Category 2: 33.3% of the total 30%
Sub Category 3: 33.3% of the total 30%
How would I make the first equation ignore 0% or blanks?
I would use the IFBlank function
how to calculate sum of basic salary of even no. of employee in excel
Hello,
For me to understand the problem better, please send me a small sample workbook with your source data and the result you expect to get to support@ablebits.com. Please don't worry if you have confidential information there, we never disclose the data we get from our customers and delete it as soon as the problem is resolved.
Please also don't forget to include the link to this comment into your email.
I'll look into your task and try to help.
KG KG EUR
0 2 2.8
2.01 5 3.2
5.01 10 3.8
10.01 3
more than 10kg i charge every 10kg 3 euros.
what formula i have to use to find the cost for the weight e.g 35kg
Hi I have 3 employees ,,, And i pay a bonus each week for the staff member who gets in the most " new sales " or "new customers".
Now i give a score of 1 point for new once off customers.
And i gave 2 points to the staff member who can get a new customer, but this new customer is a contractor and will very likely to come back for more in the future,
for example . sales Staff Peter total new sale were 1000.00 and his point score was 7.
Sales staff 2. John total new sales was 1200.00 and his point score was 5.
Sales staff 3. Sam total sales were 800 and his points score was 9.
So can you tell me who wins the bonus ?
A worker is rated on a 1-5 scale for 10 different measures and his overall skill rating is the average of these numbers. The problem is that 3 of the measures are triple weighted and to further complicate matters, its possible for a worker to not be rated at all on one of the measures. This means the value isn't a 1, but a null value not factored into the overall average so as not to penalize them. How would you formulate this in excel?
Hi, I need to average a set of course works to the original value. Let's say the course work valued 60 points but I gave 5 pieces of assignments that valued 70 points and at the end of the semester I want to average them to the original value. Usually if a student say got a total of 55 out of 70, I would calculate 55/70 X 60 = 47. So the student would get 47 out of 60. How do I put that formula in excel?
Would really appreciate your help, my class has over 60 students.
Can you replace a cell by group name in a formula? let say column A = group name and column B = $. How do you average an amount for each group not using the A1:A...but instead using Group Name such as Grapes, Peach, etc..
Thanks
Hi Svetlana,
How would I modify this to take two different sets of weights into account? Would it be wrong to multiply the 2 weights for each row?
Jo
I'm trying to use the weighted average for a group of numbers between 500,000 and 999,999. Is is possible to use the weighted average for a range of numbers. If so, how?
1.2,2.2,3.3, these numbers are in one cell in excel .but how to do sum please explain please reply soon
=SUM(A1,A2) <-- will add A1 and A2 together
=SUM(A1:A2,B1:B2) <-- will do (A1+A2)+(B1+B2)
Am tring to learn how to calculate weight average
please tell me how to calculate in excel(basic calculation,office accounts)
and also how to set calculation formats
Well I find this site very useful
How do I calculate the weight of each item
Resource Part Schedule Production Remaining Overbuild Weight
9003 3029093E 101002 88190 -12812 0
1012 3029093E-ST 94231 48290 -45941 0
1010 3035076E-ST 62374 62440 0 66
1955 3031791E-ST 28180 84020 0 55840
1958 3031330E-80S 23600 39590 0 15990
1352 3032688B-ST 16816 74700 0 57884
1350 3035077E-ST 12000 51600 0 39600
1958 3031330E-80S 6600 50000 0 43400
1350 3031413H-60S 0 49040 0 49040
how to use the same in pivot