The tutorial explains the essence of the standard deviation and standard error of the mean as well as which formula is best to be used for calculating standard deviation in Excel.
In descriptive statistics, the arithmetic mean (also called the average) and standard deviation and are two closely related concepts. But while the former is well understood by most, the latter is comprehended by few. The aim of this tutorial is shed some light on what the standard deviation actually is and how to calculate it in Excel.
What is standard deviation?
The standard deviation is a measure that indicates how much the values of the set of data deviate (spread out) from the mean. To put it differently, the standard deviation shows whether your data is close to the mean or fluctuates a lot.
The purpose of the standard deviation is to help you understand if the mean really returns a "typical" data. The closer the standard deviation is to zero, the lower the data variability and the more reliable the mean is. The standard deviation equal to 0 indicates that every value in the dataset is exactly equal to the mean. The higher the standard deviation, the more variation there is in the data and the less accurate the mean is.
To get a better idea of how this works, please have a look at the following data:
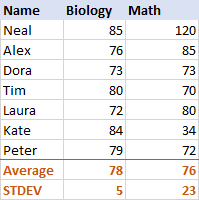
For Biology, the standard deviation is 5 (rounded to an integer), which tells us that the majority of scores are no more than 5 points away from the mean. Is that good? Well, yes, it indicates that the Biology scores of the students are pretty consistent.
For Math, the standard deviation is 23. It shows that there is a huge dispersion (spread) in the scores, meaning that some students performed much better and/or some performed far worse than the average.
In practice, the standard deviation is often used by business analysists as a measure of investment risk - the higher the standard deviation, the higher the volatility of the returns.
Sample standard deviation vs. Population standard deviation
In relation to standard deviation, you may often hear the terms "sample" and "population", which refer to the completeness of the data you are working with. The main difference is as follows:
- Population includes all of the elements from a data set.
- Sample is a subset of data that includes one or more elements from the population.
Researchers and analysists operate on the standard deviation of a sample and population in different situations. For example, when summarizing the exam scores of a class of students, a teacher will use the population standard deviation. Statisticians calculating the national SAT average score would use a sample standard deviation because they are presented with the data from a sample only, not from the entire population.
Understanding the standard deviation formula
The reason the nature of the data matters is because the population standard deviation and sample standard deviation are calculated with slightly different formulas:
Sample standard deviation |
Population standard deviation |
Where:
- xi are individual values in the set of data
- x is the mean of all x values
- n is the total number of x values in the data set
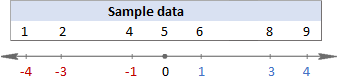
Having difficulties with understanding the formulas? Breaking them down into simple steps might help. But first, let us have some sample data to work on:

1. Calculate the mean (average)
First, you find the mean of all values in the data set (x in the formulas above). When calculating by hand, you add up the numbers and then divide the sum by the count of those numbers, like this:
(1+2+4+5+6+8+9)/7=5
To find mean in Excel, use the AVERAGE function, e.g. =AVERAGE(A2:G2)
2. For each number, subtract the mean and square the result
This is the part of the standard deviation formula that says: (xi - x)2
To visualize what's actually going on, please have a look at the following images.
In this example, the mean is 5, so we calculate the difference between each data point and 5.
Then, you square the differences, turning them all into positive numbers:
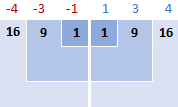
3. Add up squared differences
To say "sum things up" in mathematics, you use sigma Σ. So, what we do now is add up the squared differences to complete this part of the formula: Σ(xi - x)2
16 + 9 + 1 + 1 + 9 + 16 = 52
4. Divide the total squared differences by the count of values
So far, the sample standard deviation and population standard deviation formulas have been identical. At this point, they are different.
For the sample standard deviation, you get the sample variance by dividing the total squared differences by the sample size minus 1:
52 / (7-1) = 8.67
For the population standard deviation, you find the mean of squared differences by dividing the total squared differences by their count:
52 / 7 = 7.43
Why this difference in the formulas? Because in the sample standard deviation formula, you need to correct the bias in the estimation of a sample mean instead of the true population mean. And you do this by using n - 1 instead of n, which is called Bessel's correction.
5. Take the square root
Finally, take the square root of the above numbers, and you will get your standard deviation (in the below equations, rounded to 2 decimal places):
| Sample standard deviation | Population standard deviation |
| √8.67 = 2.94 | √7.43 = 2.73 |
In Microsoft Excel, standard deviation is computed in the same way, but all of the above calculations are performed behind the scene. The key thing for you is to choose a proper standard deviation function, about which the following section will give you some clues.
How to calculate standard deviation in Excel
Overall, there are six different functions to find standard deviation in Excel. Which one to use depends primarily on the nature of the data you are working with - whether it is the entire population or a sample.
Functions to calculate sample standard deviation in Excel
To calculate standard deviation based on a sample, use one of the following formulas (all of them are based on the "n-1" method described above).
Excel STDEV function
STDEV(number1,[number2],…) is the oldest Excel function to estimates standard deviation based on a sample, and it is available in all versions of Excel 2003 to 2019.
In Excel 2007 and later, STDEV can accept up to 255 arguments that can be represented by numbers, arrays, named ranges or references to cells containing numbers. In Excel 2003, the function can only accept up to 30 arguments.
Logical values and text representations of numbers supplied directly in the list of arguments are counted. In arrays and references, only numbers are counted; empty cells, logical values of TRUE and FALSE, text and error values are ignored.
Note. Excel STDEV is an outdated function, which is kept in the newer versions of Excel for backward compatibility only. However, Microsoft makes no promises regarding the future versions. So, in Excel 2010 and later, it is recommended to use STDEV.S instead of STDEV.
Excel STDEV.S function
STDEV.S(number1,[number2],…) is an improved version of STDEV, introduced in Excel 2010.
Like STDEV, the STDEV.S function calculates the sample standard deviation of a set of values based on the classic sample standard deviation formula discussed in the previous section.
Excel STDEVA function
STDEVA(value1, [value2], …) is another function to calculate standard deviation of a sample in Excel. It differs from the above two only in the way it handles logical and text values:
- All logical values are counted, whether they are contained within arrays or references, or typed directly into the list of arguments (TRUE evaluates as 1, FALSE evaluate as 0).
- Text values within arrays or reference arguments are counted as 0, including empty strings (""), text representations of numbers, and any other text. Text representations of numbers supplied directly in the list of arguments are counted as the numbers they represent (here's a formula example).
- Empty cells are ignored.
Note. For a sample standard deviation formula to work correctly, the supplied arguments must contain at least two numeric values, otherwise the #DIV/0! error is returned.
Functions to calculate population standard deviation in Excel
If you are dealing with the entire population, use one of the following function to do standard deviation in Excel. These functions are based on the "n" method.
Excel STDEVP function
STDEVP(number1,[number2],…) is the old Excel function to find standard deviation of a population.
In the new versions of Excel 2010, 2013, 2016 and 2019, it is replaced with the improved STDEV.P function, but is still kept for backward compatibility.
Excel STDEV.P function
STDEV.P(number1,[number2],…) is the modern version of the STDEVP function that provides an improved accuracy. It is available in Excel 2010 and later versions.
Like their sample standard deviation counterparts, within arrays or reference arguments, the STDEVP and STDEV.P functions count only numbers. In the list of arguments, they also count logical values and text representations of numbers.
Excel STDEVPA function
STDEVPA(value1, [value2], …) calculates standard deviation of a population, including text and logical values. With regard to non-numeric values, STDEVPA works exactly like the STDEVA function does.
Note. Whichever Excel standard deviation formula you use, it will return an error if one or more arguments contain an error value returned by another function or text that cannot be interpreted as a number.
Which Excel standard deviation function to use?
A variety of standard deviation functions in Excel can definitely cause a mess, especially to unexperienced users. To choose the correct standard deviation formula for a particular task, just answer the following 3 questions:
- Do you calculate standard deviation of a sample or population?
- What Excel version do you use?
- Does your data set include only numbers or logical values and text as well?
To calculate standard deviation based on a numeric sample, use the STDEV.S function in Excel 2010 and later; STDEV in Excel 2007 and earlier.
To find standard deviation of a population, use the STDEV.P function in Excel 2010 and later; STDEVP in Excel 2007 and earlier.
If you want logical or text values to be included in the calculation, use either STDEVA (sample standard deviation) or STDEVPA (population standard deviation). While I can't think of any scenario in which either function can be useful on its own, they may come in handy in bigger formulas, where one or more arguments are returned by other functions as logical values or text representations of numbers.
To help you decide which of the Excel standard deviation functions is best suited for your needs, please review the following table that summarizes the information you've already learned.
| STDEV | STDEV.S | STDEVP | STDEV.P | STDEVA | STDEVPA | |
| Excel version | 2003 - 2019 | 2010 - 2019 | 2003 - 2019 | 2010 - 2019 | 2003 - 2019 | 2003 - 2019 |
| Sample | ✓ | ✓ | ✓ | |||
| Population | ✓ | ✓ | ✓ | |||
| Logical values in arrays or references | Ignored | Evaluated (TRUE=1, FALSE=0) |
||||
| Text in arrays or references | Ignored | Evaluated as zero | ||||
| Logical values and "text-numbers" in the list of arguments | Evaluated (TRUE=1, FALSE=0) |
|||||
| Empty cells | Ignored | |||||
Excel standard deviation formula examples
Once you have chosen the function that corresponds to your data type, there should be no difficulties in writing the formula - the syntax is so plain and transparent that it leaves no room for errors :) The following examples demonstrate a couple of Excel standard deviation formulas in action.
Calculating standard deviation of a sample and population
Depending on the nature of your data, use one of the following formulas:
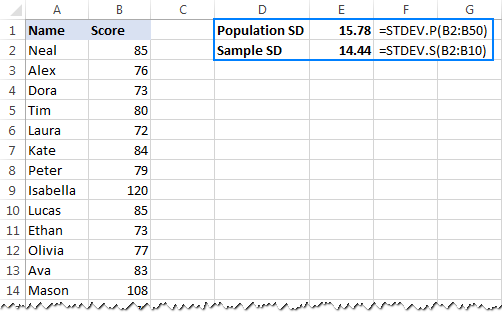
- To calculate standard deviation based on the entire population, i.e. the full list of values (B2:B50 in this example), use the STDEV.P function:
=STDEV.P(B2:B50) - To find standard deviation based on a sample that constitutes a part, or subset, of the population (B2:B10 in this example), use the STDEV.S function:
=STDEV.S(B2:B10)
As you can see in the screenshot below, the formulas return slightly different numbers (the smaller a sample, the bigger a difference):
In Excel 2007 and lower, you'd use STDEVP and STDEV functions instead:
- To get population standard deviation:
=STDEVP(B2:B50) - To calculate sample standard deviation:
=STDEV(B2:B10)
Calculating standard deviation for text representations of numbers
When discussing different functions to calculate standard deviation in Excel, we sometimes mentioned "text representations of numbers" and you might be curious to know what that actually means.
In this context, "text representations of numbers" are simply numbers formatted as text. How can such numbers appear in your worksheets? Most often, they are exported from external sources. Or, returned by so-called Text functions that are designed to manipulate text strings, e.g. TEXT, MID, RIGHT, LEFT, etc. Some of those functions can work with numbers too, but their output is always text, even if it looks much like a number.
To better illustrate the point, please consider the following example. Supposing you have a column of product codes like "Jeans-105" where the digits after a hyphen denote the quantity. Your goal is to extract the quantity of each item, and then find the standard deviation of the extracted numbers.
Pulling the quantity to another column is not a problem:
=RIGHT(A2,LEN(A2)-SEARCH("-",A2,1))
The problem is that using an Excel standard deviation formula on the extracted numbers returns either #DIV/0! or 0 like shown in the screenshot below:
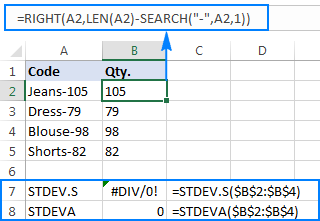
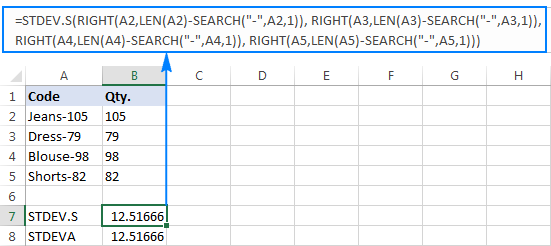
Why such weird results? As mentioned above, the output of the RIGHT function is always a text string. But neither STDEV.S nor STDEVA can handle numbers formatted as text in references (the former simply ignores them while the latter counts as zeros). To get the standard deviation of such "text-numbers", you need to supply them directly to the list of arguments, which can be done by embedding all RIGHT functions into your STDEV.S or STDEVA formula:
=STDEV.S(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1)))
=STDEVA(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1)))
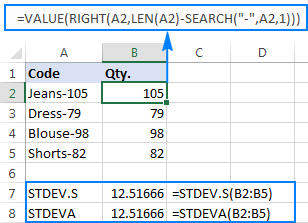
The formulas are a bit cumbersome, but that might be a working solution for a small sample. For a bigger one, not to mention the entire population, it is definitely not an option. In this case, a more elegant solution would be having the VALUE function convert "text-numbers" to numbers that any standard deviation formula can understand (please notice the right-aligned numbers in the screenshot below as opposed to the left-aligned text strings on the screenshot above):
How to add standard deviation bars in Excel
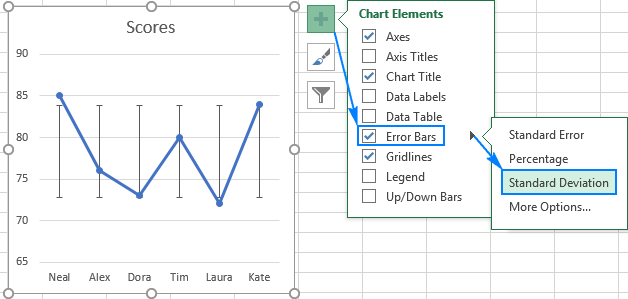
To visually display a margin of the standard deviation, you can add standard deviation bars to your Excel chart. Here's how:
- Create a graph in the usual way (Insert tab > Charts group).
- Click anywhere on the graph to select it, then click the Chart Elements button.
- Click the arrow next to Error Bars, and pick Standard Deviation.
This will insert the same error bars for all data points.
For more information, see How to add error bars to Excel charts.
Standard deviation vs. standard error of the mean
In statistics, there is one more measure for estimating the variability in data - standard error of mean, which is sometimes shortened (though, incorrectly) to just "standard error". The standard deviation and standard error of the mean are two closely related concepts, but not the same.
While the standard deviation measures the variability of a data set from the mean, the standard error of the mean (SEM) estimates how far the sample mean is likely to be from the true population mean. Said another way - if you took multiple samples from the same population, the standard error of the mean would show the dispersion between those sample means. Because usually we calculate just one mean for a set of data, not multiple means, the standard error of the mean is estimated rather than measured. The standard deviation is always bigger than SEM.
The standard error is the ratio of the standard deviation to the square root of the sample size. In your Excel worksheets, you can calculate it by using the STDEV.S function together with COUNT and SQRT. The generic formula is:
Assuming the sample data are in B2:B10, our SEM formula would go as follows:
=STDEV.S(B2:B10)/SQRT(COUNT(B2:B10))
And the result might be similar to this:
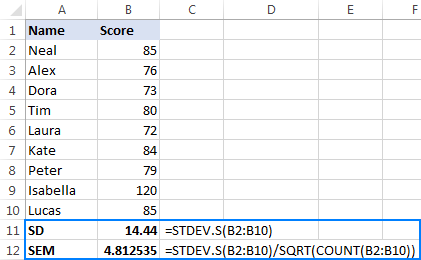
For more information, see How to calculate standard error of the mean in Excel.
This is how to do standard deviation on Excel. I hope you will find this information helpful. Anyway, I thank you for reading and hope to see you on our blog next week.
 by
by
27 comments
thanks for great topic for sd
Lets say I had a construction project, that will cost $80. How could I use the standard deviation to calculate what the expenses will be over 5 of months?
ie. first month is $5, second is $10, Third is $50, fourth is $10 and fifth is $5?
Sorry this wasnt explained properly.
Lets say I have $100 dollars to spend, how can I find out how it would be distributed/spent using a standard deviation model in excel?
Good & Easy way to understood
Let's say, sticking to the first example of "Biology and Math", I want to calculate the standard deviation only on Math with respect on Biology.
So want I want to know is the spread out of Math compared to Biology.
How would that be possible to calculate?
Thank you very much
Hello!
The STDEV function cannot calculate your issue. Calculate using the standard deviation formula from the first paragraph.
THANK YOU
Great explanation and simple. thank you
Thanks for all
Very simple way of explanation. thank you.
I need to calculate the standard deviation of a column of data ONLY if the date is filled in another column. In another words some of the cells in the date column (column O) are empty meaning the data is "0.0000" in the column (column I) in which I want to calculate the standard deviation. My goal is to eliminate the "0.0000" from the standard deviation calculation.
I used the formula =STDEV(IF(O2:O325,"",I2:I325) One row for header and 324 rows of data. It seems to work in one spreadsheet of the workbook but does not transfer to the other 150+ sheets. Also, in the spreadsheet that it did work on, the formula will not copy over to the other 5 columns (J, K, L, M, N) that need the same calculation.
Any help is very much appreciated.
Please email me if more information is needed.
Thank you,
Gene
How do calculate the deviation from the average for each data point
Thanks, you have cleared all the confusions regarding different forms and versions used in Excel.
i have a data set of 200 subjects. outcomes of the data set are either '1' or '0'...
True or False basically. 50 trues in data set and 150 false
i have filtered the data to either show the false subjects or the true subjects.
Im using the subtotal function to calculate the filtered sets.
every function i need for my filtered set returns the correct values except for when I use the STDEV.P
STDEV.P calculates the entire data set including the non visible filtered out data.
how do I simply make that subtotal cell perform STDEV.P on just my shown filtered data???
this one is killing me.... HELP???
How can I limit my standard deviation (SD) bar.....say for example the maximum score that can be obtained by a student is 100 only.....but the mean of classes' score is 95 with a SD of 10 meaning overall score would be 95±10. But as the score cannot be greater than 100, 95+10 is wrong so the upper limit of SD should have been restricted to 5.
Following this, I am asking is there a way to automatically restrict the upper limit of the SD bar in excel or not???
please respond asap.
Q. How to calculate the statistic S y/x, which estimates the random errors in the y-direction by used excel
I'm looking for formula wherein I need to calculate Standard Deviation only for selected criteria. Like I have A B C D and those A B C D are available in my table from where I need to pull respective numbers. So I need to calculate standard dev. for A separately, B separately and so on... Also, need to take care of excluding Zeros 0. Presently I'm using below formula.
=IFERROR(STDEV.P(IF(ISNUMBER(1/D4:D88),IF(D4:D88>0,D4:D88))),"-")
I need to add comparison to it.
Thanks a bunch...
Extremely clear and comprehensive. Not everybody that knows this stuff can explain it as straightforwardly as this! Great work!
PROF. You are a great lecturer, I am grateful to grab a bit knowledge from you within this few seconds.my regard to u.
Thanks this has been really helpful. Can you tell me does excel calculate Stdev.s or Stdev.p when you add “Standard Deviation” from “error bars” in “Add chart element” ?
Hi Libby,
For error bars, Excel actually calculates standard deviation as a single value form the given Y-values, assuming that the Y-values are individual values from one sample. As the result, the default error bars drawn by Excel are the same for all data points in a series. The formula that Excel uses for calculating standard deviation error bars can be found here.
If you'd like to plot individual Std Dev error bars, you can first calculate Stdev.s or Stdev.p, depending on your data set. And then, on your chart, click Error Bars > More Options >Custom, and select the range of the calculated Std Dev values. An example can be found here: How to make individual error bars in Excel.
Hello
I have to calculate the standard deviation of the centre of pressure displacement which expresses the variability of the centre of pressure at specific points in time. I will do the calculations in excel, however, I would like to know is the standard deviation formula the same for any variable for which SD is used?
Hi, I'm trying to come up with a formula that copies contents of a cell only if the value of that cell being copied is -1 or less, then converts copied negative number to a positive value. A Here's a formula I tried =if(Q2>=0,"",Q2)*-1
(P2 is copying data from Q2) but instead if leaving cell blank it displays a 0. How do you think I should change the formula to have a cell stay blank instead of populating it with 0?
If anyone is also wondering it was as simple as moving *-1 inside parentheses
=if(Q2>=0,"",Q2*-1)