The tutorial explains how to use Excel FORECAST and other related functions with formula examples.
In Microsoft Excel, there are several functions that can help you create linear and exponential smoothing forecasts based on historical data such as sales, budgets, cash flows, stock prices, and the like.
The main focus of this tutorial will be on the two main forecasting functions, but we will touch briefly on other functions as well to help you understand their purpose and basic uses.
Excel forecasting functions
In the recent versions of Excel, there exist six different forecasting functions.
The two functions do linear forecasts:
- FORECAST - predicts future values by using linear regression; a legacy function for backwards compatibility with Excel 2013 and earlier.
- LINEAR - identical to the FORECAST function; part of the new suite of forecasting functions in Excel 2016 and Excel 2019.
The four ETS functions are purposed for exponential smoothing forecasts. These functions are only available in Excel for Office 365, Excel 2019, and Excel 2016.
- ETS - predicts future values based on the exponential smoothing algorithm.
- ETS.CONFINT - calculates the confidence interval.
- ETS.SEASONALITY - calculates the length of a seasonal or other recurring pattern.
- ETS.STAT - returns statistical values for time series forecasting.
Excel FORECAST function
The FORECAST function in Excel is used to predict a future value by using linear regression. In other words, FORECAST projects a future value along a line of best fit based on historical data.
The syntax of the FORECAST function is as follows:
Where:
- X (required) - a numerical x-value for which you want to predict a new y-value.
- Known_y's (required) - an array of known dependent y-values.
- Known_x's (required) - an array of known independent x-values.
The FORECAST function works in all versions of Excel for Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003, Excel XP, and Excel 2000.
Note. In Excel 2016 and 2019, this function has been replaced with FORECAST.LINEAR, but is still available for backward compatibility.
Excel FORECAST.LINEAR function
The FORECAST.LINEAR function is the modern counterpart of the FORECAST function. It has the same purpose and syntax:
This function is available in Excel for Office 365, Excel 2019, and Excel 2016.
How FORECAST and FORECAST.LINEAR calculate future values
Both functions calculate a future y-value by using the linear regression equation:
y = a + bx
Where the a constant (intercept) is:
![]()
And the b coefficient (slope of the line) is:
![]()
The values of x̄ and ȳ are the sample means (averages) of the known x-values and y-values.
Excel FORECAST function not working:
If your FORECAST formula returns an error, this is most likely because of the following reasons:
- If the known_x's and known_y's ranges are of different lengths or empty, the #N/A! error occurs.
- If the x value is non-numeric, the formula returns the #VALUE! error.
- If the variance of known_x's is zero, the #DIV/0! error occurs.
How to use FORECAST function in Excel - formula example
As already mentioned, the Excel FORECAST and FORECAST.LINEAR functions are purposed for linear trend forecasting. They work best for linear datasets and in situations when you want to forecast a general trend ignoring insignificant data fluctuations.
As an example, we will try to predict our web-site traffic for the next 7 days based on the data for the previous 3 weeks.
With the known y-values (no. of visitors) in B2:B22 and the known x-values (dates) in A2:A22, the forecast formula goes as follows.
Excel 2019 - Excel 2000:
=FORECAST(A23, $B$2:$B$22, $A$2:$A$22)
Excel 2016 and Excel 2019:
=FORECAST.LINEAR(A23, $B$2:$B$22, $A$2:$A$22)
Where A23 is a new x-value for which you wish to predict a future y-value.
Depending on your Excel version, insert one of the above formulas in any empty cell in row 23, copy it down to as many cells as needed and you will get this result:
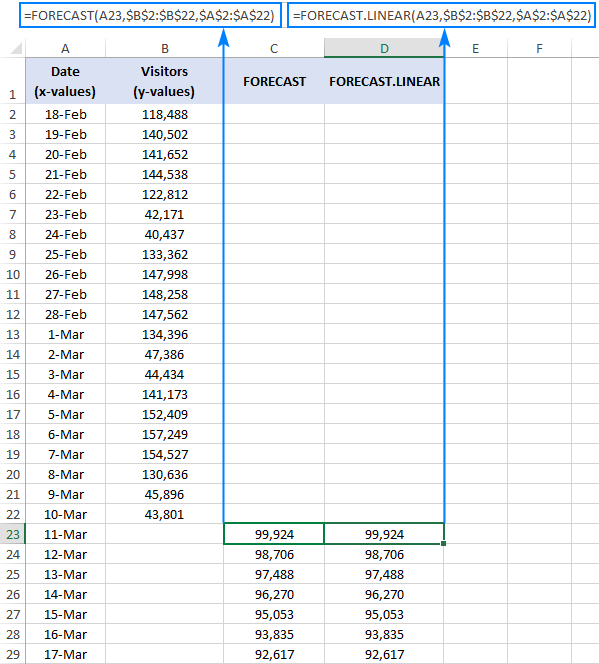
Please pay attention that we lock the ranges with absolute cell references (like $A$2:$A$2) to prevent them from changing when copying the formula to other cells.
Plotted on a graph, our linear forecast looks as follows:

The detailed steps to make such a graph are described in Linear regression forecasting chart.
If you'd like to predict future values based on the recurring pattern observed in your historical data, then use FORECAST.ETS instead of the Excel FORECAST function. And the next section of our tutorial shows how to do this.
Excel FORECAST.ETS function
The FORECAST.ETS function is used to do exponential smoothing forecasts based on a series of existing values.
More precisely, it predicts a future value based on the AAA version of the Exponential Triple Smoothing (ETS) algorithm, hence the function's name. This algorithm smoothes out insignificant deviations in data trends by detecting seasonality patterns and confidence intervals. "AAA" stands for additive error, additive trend and additive seasonality.
The FORECAST.ETS function is available in Excel for Office 365, Excel 2019, and Excel 2016.
The syntax of the Excel FORECAST.ETS is as follows:
Where:
- Target_date (required) - the data point for which to forecast a value. It can be represented by a date/time or number.
- Values (required) - a range or array of historical data for which you want to predict future values.
- Timeline (required) - an array of dates/times or independent numeric data with a constant step between them.
- Seasonality (optional) - a number representing the length of the seasonal pattern:
- 1 or omitted (default) - Excel detects seasonality automatically by using positive, whole numbers.
- 0 - no seasonality, i.e. a linear forecast.
The maximum allowed seasonality is 8,760, which is the number of hours in a year. A higher seasonality number will result in the #NUM! error.
- Data completion (optional) - accounts for missing points.
- 1 or omitted (default) - fill in the missing points as the average of the neighboring points (liner inrerpolation).
- 0 - treat the missing points as zeros.
- Aggregation (optional) - specifies how to aggregate multiple data values with the same time stamp.
- 1 or omitted (default) - the AVERAGE function is used for aggregation.
- Your other options are: 2 - COUNT, 3 - COUNTA, 4 - MAX, 5 - MEDIAN, 6 - MIN and 7 - SUM.
5 things you should know about FORECAST.ETS
- For the correct work of the FORECAST.ETS function, the timeline should have a regular interval - hourly, daily, monthly, quarterly, yearly, etc.
- The function is best suited for non-linear data sets with seasonal or other repetitive pattern.
- When Excel cannot detect a pattern, the function reverts to a linear forecast.
- The function can work with incomplete datasets where up to 30% data points are missing. The missing points are treated according to the value of the data completion argument.
- Although a timeline with a consistent step is required, there may be duplicates in the date/time series. The values with the same timestamp are aggregated as defined by the aggregation argument.
FORECAST.ETS function not working:
If your formula produces an error, this is likely to be one of the following:
- The #N/A occurs if the values and timeline arrays have different length.
- The #VALUE! error is returned if the seasonality, data completion or aggregation argument is non-numeric.
- The #NUM! error may be thrown because of the following reasons:
- A consistent step size cannot be detected in timeline.
- The seasonality value is out of the supported range (0 - 8,7600).
- The data completion value is other than 0 or 1.
- The aggregation value is out of the valid range (1 - 7).
How to use FORECAST.ETS function in Excel - formula example
To see how the future values calculated with exponential smoothing are different from a linear regression forecast, let's make a FORECAST.ETS formula for the same data set that we used in the previous example:
Where:
- A23 is the target date
- $B$2:$B$22 are the historical data (values)
- $A$2:$A$22 are the dates (timeline)
By omitting the last three arguments (seasonality, data completion or aggregation) we rely on Excel defaults. And Excel forecasts the trend perfectly:

Excel FORECAST.ETS.CONFINT function
The FORECAST.ETS.CONFINT function is used to calculate the confidence interval for a forecasted value.
The confidence interval is kind of a measure of the prediction accuracy. The smaller the interval, the more confidence in the prediction for a specific data point.
The FORECAST.ETS.CONFINT is available in Excel for Office 365, Excel 2019, and Excel 2016.
The function has the following arguments:
As you see, the syntax of FORECAST.ETS.CONFINT is very similar to that of the FORECAST.ETS function, except this additional argument:
Confidence_level (optional) - a number between 0 and 1 that specifies a level of confidence for the calculated interval. Typically, it is supplied as a decimal number, though percentages are also accepted. For instance, to set a 90% confidence level, you enter either 0.9 or 90%.
- If omitted, the default value of 95% is used, meaning that 95% of the time a predicted data point is expected to fall within this radius from the value returned by FORECAST.ETS.
- If the confidence level is outside of the supported range (0 - 1), the formula returns the #NUM! error.
FORECAST.ETS.CONFINT formula example
To see how it works in practice, let's calculate the confidence interval for our sample data set:
=FORECAST.ETS.CONFINT(A23, $B$2:$B$22, $A$2:$A$22)
Where:
- A23 is the target date
- $B$2:$B$22 are the historical data
- $A$2:$A$22 are the dates
The last 4 arguments are omitted, telling Excel to use the default options:
- Set the confidence level to 95%.
- Detect seasonality automatically.
- Complete missing points as the average of the neighboring points.
- Aggregate multiple data values with the same timestamp by using the AVERAGE function.
To grasp what the returned values actually mean, please take a look at the screenshot below (some rows with historical data are hidden for the sake of space).
The formula in D23 gives the result 6441.22 (rounded to 2 decimal points). What it means is that 95% of the time, the prediction for 11-Mar is expected to fall within 6441.22 of the forecasted value 61,075 (C3). That is 61,075 ± 6441.22.

To find out the range within which the forecasted values are likely to fall, you can calculate the confidence interval bounds for each data point.
To get the lower bound, subtract the confidence interval from the forecasted value:
=C23-D23
To get the upper bound, add the confidence interval to the forecasted value:
=C23+D23
Where C23 is the predicted value returned by FORECAST.ETS and D23 is the confidence interval returned by FORECAST.ETS.CONFINT.
Copy the above formulas down, plot the results on a chart, and you will have a clear visual representation of the predicted values and the confidence interval:

Tip. To have such a graph created for you automatically, leverage the Excel Forecast Sheet feature.
Excel FORECAST.ETS.SEASONALITY function
The FORECAST.ETS.SEASONALITY function is used to calculate the length of a recurring pattern in the specified timeline. It is closely tied with FORECAST.ETS because both functions use the same algorithm to detect seasonality.
This function is available in Excel for Office 365, Excel 2019, and Excel 2016.
The syntax of FORECAST.ETS.SEASONALITY is as follows:
For our data set, the formula takes the following shape:
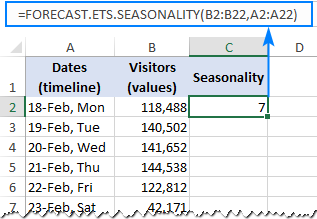
=FORECAST.ETS.SEASONALITY(B2:B22, A2:A22)
And returns the seasonality 7, which perfectly agrees with the weekly pattern of our historical data:
Excel FORECAST.ETS.STAT function
The FORECAST.ETS.STAT function in returns a specified statistical value relating to a time series exponential smoothing forecasting.
Like other ETS functions, it is available in Excel for Office 365, Excel 2019, and Excel 2016.
The function has the following syntax:
The statistic_type argument indicates which statistical value to return:
- Alpha (base value) - the smoothing value between 0 and 1 that controls the weighting of data points. The higher the value, the more weight is given to recent data.
- Beta (trend value) - the value between 0 and 1 that determines the trend calculation. The higher the value, the more weight is given to recent trends.
- Gamma (seasonality value) - the value between 0 and 1 that controls the seasonality of the ETS forecast. The higher the value, the more weight is given to the recent seasonal period.
- MASE (mean absolute scaled error) - a measure of the forecast accuracy.
- SMAPE (symmetric mean absolute percentage error) - a measure of accuracy based on percentage or relative errors.
- MAE (mean absolute error) - measures the average magnitude of the prediction errors, regardless of their direction.
- RMSE (root mean square error) - a measure of the differences between the predicted and observed values.
- Step size detected - the step size detected in the timeline.
For example, to return the Alpha parameter for our sample data set, we use this formula:
=FORECAST.ETS.STAT(B2:B22, A2:A22, 1)
The screenshot below shows the formulas for other statistical values:

That's how you do time series forecasting in Excel. To investigate all the formulas discussed in this tutorial, you are welcome to download our sample workbook below. I thank you for reading and hope to see you on our blog next week!
Practice workbook for download
Excel Forecast formula examples (.xlsx file)
 by
by
22 comments
How calculate the forecast if the data are in more than one sheet ? (I cannot put all of them in a single sheet)
The formula seems don't work
Thanks
Hello Agostino!
You can combine multiple arrays of values from multiple worksheets using VSTACK function. The formula might look like this:
=FORECAST(A23,VSTACK('2'!$B$2:$B$22,'1'!B2:B22),VSTACK('2'!$A$2:$A$22,'1'!A2:A22))
For more information, please visit: Combine ranges and arrays in Excel: VSTACK & HSTACK functions.
Hello,
In your example of the forecasting.ETS your are not taking the full history from cell 2 to cell 22 but: =FORECAST.ETS(C23;B$2:B$15;C$2:C$15). Why is this?
And what is the formula for the cell below to become 152,753? It is not =FORECAST.ETS(C24;B$2:B$15;C$2:C$15)
Hello Kristian,
Of course, we should take the full history from rows 2 to 22. The formula in the text of that example is correct, but in the image and in the sample workbook, the formula was wrong. I cannot say how that could happen, perhaps I accidentally changed the range when capturing the screenshot.
Only the formula in C23 was referring to a wrong range. In all other cells, the formulas were correct. In cell C24, the formula is =FORECAST.ETS(C24; B$2:B$22; C$2:C$22) and it returns 152,753.
Anyway, the screenshot is fixed and shows the correct formula now. Thank you very much for pointing that out and my sincere apologies for the confusion.
Sorry typo above, it should say =FORECAST.ETS(A23;B$2:B$15;A$2:A$15
hello i am currently working with covid-19 data and i would like to predict the positive cases in the coming months based on the data i have. can you please help me out ?? what Forecast function should I use??
Hello!
Have you tried the ways described in this blog post? If they don’t work for you, then please describe your task in detail, I’ll try to suggest a solution.
Hi,
We receive two results when we are putting "FORECAST(x, known_y's, known_x's)" function with and without absolute reference. Which one is correct?
Sir, is it possible to give the detail on formula that needs to be used if someone has to achieve this value manually.
Using Excel in Windows 7 Using Forecast function - - worked well on spreadsheet for 3 yrs of data, but today, next date, getting a 1 digit number - - totally out of line with the series (index going to 7.1 next week, from a month-long series of values in the 300's. Cell shows a error spot upper left corner, but have tried all the "fixes" inside the "formula bar" and nothing works.
Please sir my question is outline the basic steps involved in using Ms Excel forecast function . Thank you sir
Hi,
I tried and tested these functions on my requirement to identify the future date when a certain value is reached. However, some showed past dates instead of future dates. What am I missing here?
Hi Svetlana,
Can we use FORECAST.ETS.CONFINT to calculate confidence interval for FORECAST or FORECAST.LINEAR function.
Thanks
Use the summary statistics in the data validation tab.
I had a set of daily sales values. I forecasted based on the Office 365 data tab's forecast function icon. I put in a 99% confidence interval. It turned out a lower confidence Bound that had minus values. However, I know for sure in reality, these values cannot be possible. How can I change the setting to obtain values that are only positive and how can I change the setting to exclude the - values on the axis in my scenario?
Due to this turnout, I do not even dare to use this function.
Hi,
What formula we can use to incorporate growth in the forecast formula?
Hi,
I am exploring forcast.linear and not able to get the results in Nov-19 column.
Here's my data set
Col A Col B Col C Col D Col E Col F Col G Col H Col I
R1 Category Description Apr-18 May-18 Jul-19 Aug-19 Sep-19 Oct-19 Nov-19
R2 Food Biscuit 2 2 7 3 2 3 0
R3 Food Tea 2 1 2 0 0 0 0
R4 Food Coffee 5 4 15 7 6 12 0
R5 Food Cup Noodles 10 15 16 10 5 20 0
My formula is "=FORECAST.LINEAR(I2,$C2:$H2,$C1:$H1)"
What went wrong?
April and May year in 2018. and from Jul it's 19. give symmetrically spaced data.
zdorovatsya Svetlana,
thanks so much for your great effort in explaining Excel formulas, it really helps.
my question is which is better absolute or relative reference cell while using various forecasting functions ?? because each reference generates different forecasted figures and I am building a forecasting model for my department budget and I am a little hesitated to choose the accurate reference.
T
Hi Ahmed,
Generally, the choice of the cell reference type is determined by the structure of your data, which is why it's impossible to give any advice without seeing how your data is organized. Hopefully, the following article will help you get clear understanding of how Excel cell references work: Absolute and relative cell references in Excel.
I DON'T UNDERSTAND THESE FUNCTIONS.
Good one.