How to calculate standard error of the mean in Excel

Standard error of the mean

Standard error of the mean (SEM), which is sometimes shortened to just standard error (SE), is a measure of the variability of the sample mean from the population mean.

In other words, the SEM measures how much variation there is likely to be between different samples taken from the same population, and how accurately the sample mean represents the true population mean. Looking from another angle, the standard error measures the amount of error that can be expected in the sample mean when repeated samples are taken from the same population.

In mathematics, the standard error of the mean is typically calculated as the ratio of the standard deviation to the square root of the sample size.

Where SD is the standard deviation, and n is the number of observations in the sample.

Microsoft Excel has its own way of calculating the standard error, which we will discuss in more detail a bit later.

Importance of standard error calculation

When taking multiple samples from the same data set, calculating the standard error of the mean is important because it provides an estimation of their reliability. A smaller standard error indicates that the sample means are more likely to be close to the true population mean, while a larger standard error suggests greater uncertainty in the estimates. So, the smaller the standard error, the more you can trust the accuracy of the sample.

The SEM is particularly valuable in scientific research because it can be used to test hypotheses and determine the statistical significance of results. For example, researchers might compare the sample means of two groups and calculate the standard error of the mean to determine if the difference between the groups is likely due to chance or reflects a real difference in the population.

Overall, by providing a measure of the precision and accuracy of sample estimates, the standard error helps researchers draw more meaningful conclusions from their data. It guides decisions about sample size and statistical power, leading to more robust and reliable research findings.

How to calculate standard error of the mean in Excel

Given that the standard error is equal to the standard deviation divided by the square root of the number of observations, Excel offers a simple way to get the SEM by using a combination of three different functions.

To calculate the standard error of the mean in Excel, carry out these steps:

1. Enter the data into an Excel worksheet organizing it into rows or columns.
2. Calculate the sample standard deviation using the STDEV.S function.
3. Get the sample size, i.e. the total number of values, with the help of the COUNT function.
4. Determine the square root of the sample size using the SQRT function.
5. Divide the standard deviation by the square root of the sample size.

The generic formula for calculating the SEM in Excel is as follows:

Where range is the range of cells containing your data.

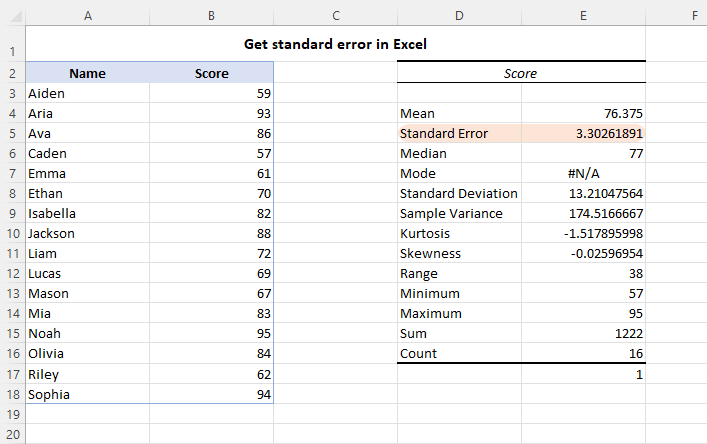
Assuming the sample data is in B2:B18, our Excel standard error formula would go as follows:

=STDEV.S(B3:B18)/SQRT(COUNT(B3:B18))

Once the formula is calculated, the result will resemble this:

How to find standard error using Data Analysis ToolPak

Another way to calculate the standard error of the mean in Excel is by using the Data Analysis Toolpak. To use this feature, you first need to ensure that the Toolpak is installed in your Excel. Here are the steps to Enable Analysis ToolPak add-in in Excel.

With the Data Analysis Toolpak activated, you can calculate the standard error of the mean using the following steps:

1. Enter your sample data into a column.
2. On the Data tab, in the Analysis group, click Data Analysis.
3. In the Analysis Tools dialog box, select Descriptive Statistics from the list of analysis tools and click OK.
4. In the Analysis Tools dialog box, do the following:
   • In the Input Range box, select the range of cells that contain your sample data.
   • If you've included column headers in the selection, be sure to check the Labels in first row box to ensure the data is analyzed correctly.
   • In the Output Range box, select where you want the results to appear. To avoid overwriting any existing data, it's safer to choose New Worksheet. If you prefer to display the results on the same sheet, select the upper-left cell of the destination range in a blank column and ensure there is at least one empty column to the right of it.
   • Select the checkbox next to Summary Statistics and click OK.
   

Excel will now generate a new table that contains various descriptive statistics for your sample data, including the standard error of the mean. You can verify that the standard error value exactly matches the SEM calculated with the formula, as shown in the screenshot below.

How to add standard error bars in Excel

To visually display the variability in data points and highlight the precision of the sample mean, you can add standard error bars to an Excel chart. Standard error bars show the range of values within which the sample mean is likely to fall, given a specific level of confidence.

To insert standard error bars in an Excel graph, perform these steps:

1. First, create a chart from your data. For this, select the data range, go to the Insert tab and choose the desired chart type from the Charts group.
2. Click on the chart to select it, and then click on the Chart Elements button in the upper-right corner.
3. From the drop-down menu, click the arrow next to Error Bars, and select Standard Error.

The standard error bars will be added to your chart to help you compare means between different groups and assess the significance of any observed differences.

For more details, see How to insert error bars in Excel charts.

Standard error of the mean vs. standard deviation

Standard deviation and standard error of the mean are two related statistical concepts that are often used to measure the variability of data. While they may seem similar, they have different meanings and uses.

Standard deviation (SD) measures the amount of variation or dispersion of a set of data from its mean. A high standard deviation indicates that the data points are spread out widely from the mean, while a low standard deviation suggests that the data points are close to the mean.

On the other hand, standard error of the mean (SEM) measures the variability of the sample mean from the population mean. The standard error indicates how accurately the sample mean represents the true population mean, and how much error is expected when taking multiple samples from the same population. A low SEM suggests that the sample mean is a good estimate of the population mean, while a high SEM suggests that the sample mean may not be a reliable estimate of the population mean.

The standard error of the mean is always smaller than the standard deviation because it is calculated by dividing the SD by the square root of the sample size, which reduces its value.

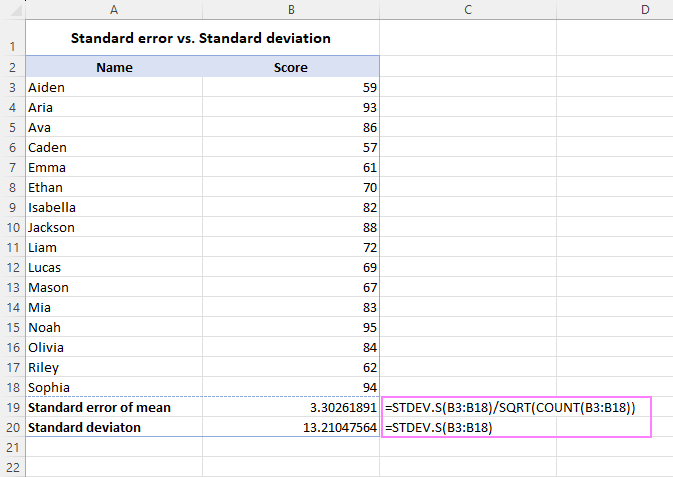
In summary, standard deviation measures the variability within a set of data, while standard error of the mean measures the variability of the sample mean from the population mean.

For more information, see how to calculate standard deviation in Excel.

Practice workbook for download

Standard error in Excel - examples (.xlsx file)