In this tutorial, we will look at how to do variance analysis Excel and what formulas to use to find variance of a sample and population.
Variance is one of the most useful tools in probability theory and statistics. In science, it describes how far each number in the data set is from the mean. In practice, it often shows how much something changes. For example, temperature near the equator has less variance than in other climate zones. In this article, we will analyze different methods of calculating variance in Excel.
What is variance?
Variance is the measure of variability of a data set that indicates how far different values are spread. Mathematically, it is defined as the average of the squared differences from the mean.
To better understand what you are actually calculating with the variance, please consider this simple example.
Supposing there are 5 tigers in your local zoo that are 14, 10, 8, 6 and 2 years old.
To find variance, follow these simple steps:
- Calculate the mean (simple average) of the five numbers:
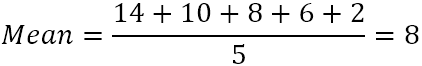
- From each number, subtract the mean to find the differences. To visualize this, let's plot the differences on the chart:
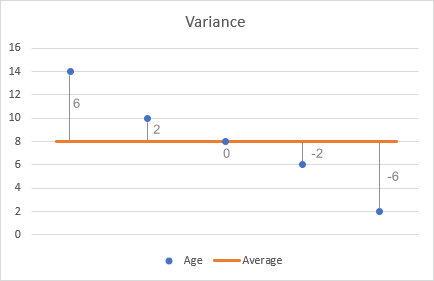
- Square each difference.
- Work out the average of the squared differences.
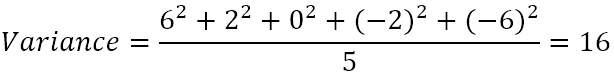
So, the variance is 16. But what does this number actually mean?
In truth, variance just gives you a very general idea of the dispersion of the data set. A value of 0 means there is no variability, i.e. all the numbers in the data set are the same. The bigger the number, the more spread out the data.
This example is for population variance (i.e. 5 tigers are the whole group you are interested in). If your data is a selection from a bigger population, then you need to calculate sample variance by using a slightly different formula.
How to calculate variance in Excel
There are 6 built-in functions to do variance in Excel: VAR, VAR.S, VARP, VAR.P, VARA, and VARPA.
Your choice of the variance formula is determined by the following factors:
- The version of Excel you are using.
- Whether you calculate sample or population variance.
- Whether you want to evaluate or ignore text and logical values.
Excel variance functions
The below table provides an overview of the variation functions available in Excel to help you choose the formula best suited for your needs.
| Name | Excel version | Data type | Text and logicals |
| VAR | 2000 - 2019 | Sample | Ignored |
| VAR.S | 2010 - 2019 | Sample | Ignored |
| VARA | 2000 - 2019 | Sample | Evaluated |
| VARP | 2000 - 2019 | Population | Ignored |
| VAR.P | 2010 - 2019 | Population | Ignored |
| VARPA | 2000 - 2019 | Population | Evaluated |
VAR.S vs. VARA and VAR.P vs. VARPA
VARA and VARPA differ from other variance functions only in the way they handle logical and text values in references. The following table provides a summary of how text representations of numbers and logical values are evaluated.
| Argument Type | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Logical values within arrays and references | Ignored | Evaluated (TRUE=1, FALSE=0) |
| Text representations of numbers within arrays and references | Ignored | Evaluated as zero |
| Logical values and text representations of numbers typed directly into arguments | Evaluated (TRUE=1, FALSE=0) |
|
| Empty cells | Ignored | |
How to calculate sample variance in Excel
A sample is a set of data extracted from the entire population. And the variance calculated from a sample is called sample variance.
For example, if you want to know how people's heights vary, it would be technically unfeasible for you to measure every person on the earth. The solution is to take a sample of the population, say 1,000 people, and estimate the heights of the whole population based on that sample.
Sample variance is calculated with this formula:
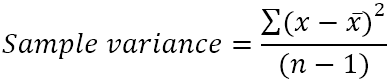
Where:
- x̄ is the mean (simple average) of the sample values.
- n is the sample size, i.e. the number of values in the sample.
There are 3 functions to find sample variance in Excel: VAR, VAR.S and VARA.
VAR function in Excel
It is the oldest Excel function to estimate variance based on a sample. The VAR function is available in all versions of Excel 2000 to 2019.
Note. In Excel 2010, the VAR function was replaced with VAR.S that provides improved accuracy. Although VAR is still available for backward compatibility, it is recommended to use VAR.S in the current versions of Excel.
VAR.S function in Excel
It is the modern counterpart of the Excel VAR function. Use the VAR.S function to find sample variance in Excel 2010 and later.
VARA function in Excel
The Excel VARA function returns a sample variance based on a set of numbers, text, and logical values as shown in this table.
Sample variance formula in Excel
When working with a numeric set of data you can use any of the above functions to calculate sample variance in Excel.
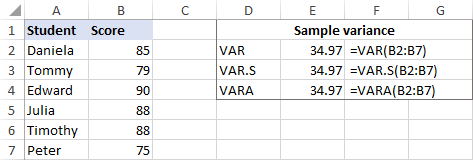
As an example, let's find the variance of a sample consisting of 6 items (B2:B7). For this, you can use one of the below formulas:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
As shown in the screenshot, all the formulas return the same result (rounded to 2 decimal places):
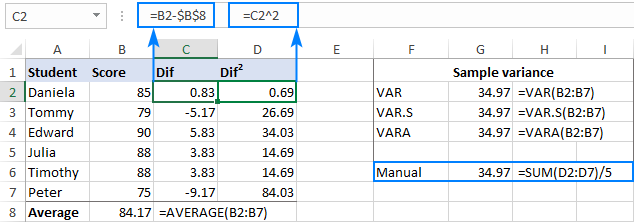
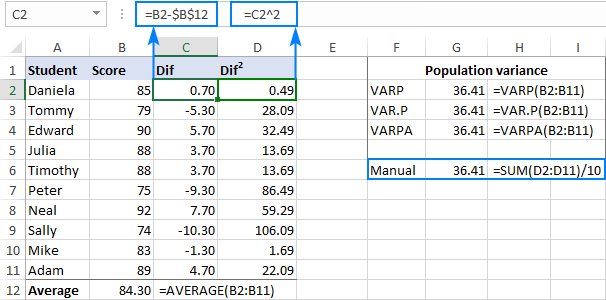
To check the result, let's do var calculation manually:
- Find the mean by using the AVERAGE function:
=AVERAGE(B2:B7)The average goes to any empty cell, say B8.
- Subtract the average from each number in the sample:
=B2-$B$8The differences go to column C, beginning in C2.
- Square each difference and put the results to column D, beginning in D2:
=C2^2 - Add up the squared differences and divide the result by the number of items in the sample minus 1:
=SUM(D2:D7)/(6-1)
As you can see, the result of our manual var calculation is exactly the same as the number returned by Excel's built-in functions:
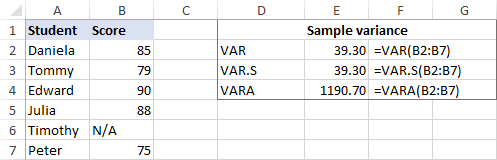
If your data set contains the Boolean and/or text values, the VARA function will return a different result. The reason is that VAR and VAR.S ignore any values other than numbers in references, while VARA evaluates text values as zeros, TRUE as 1, and FALSE as 0. So, please carefully choose the variance function for your calculations depending on whether you want to process or ignore text and logicals.
How to calculate population variance in Excel
Population is all members of a given group, i.e. all observations in the field of study. Population variance describes how data points in the entire population are spread out.
The population variance can be found with this formula:
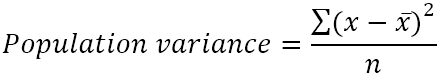
Where:
- x̄ is the mean of the population.
- n is the population size, i.e. the total number of values in the population.
There are 3 functions to calculate population variance in Excel: VARP, VAR.P and VARPA.
VARP function in Excel
The Excel VARP function returns the variance of a population based on the entire set of numbers. It is available in all versions of Excel 2000 to 2019.
Note. In Excel 2010, VARP was replaced with VAR.P but is still kept for backward compatibility. It is recommended to use VAR.P in the current versions of Excel because there is no guarantee that the VARP function will be available in future versions of Excel.
VAR.P function in Excel
It is an improved version of the VARP function available in Excel 2010 and later.
VARPA function in Excel
The VARPA function calculates the variance of a population based on the entire set of numbers, text, and logical values. It is available in all version of Excel 2000 through 2019.
Population variance formula in Excel
In the sample var calculation example, we found a variance of 5 exam scores assuming those scores were a selection from a bigger group of students. If you collect data on all the students in the group, that data will represent the entire population, and you will calculate a population variance by using the above functions.
Let's say, we have the exam scores of a group of 10 students (B2:B11). The scores constitute the entire population, so we will do variance with these formulas:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
And all the formulas will return the identical result:
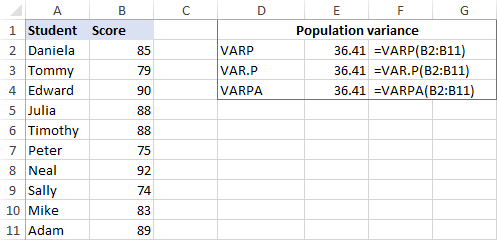
To make sure Excel has done the variance right, you can check it with the manual var calculation formula shown in the screenshot below:
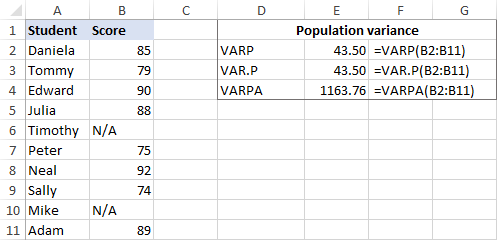
If some of the students did not take the exam and have N/A instead of a score number, the VARPA function will return a different result. The reason is that VARPA evaluates text values as zeros while VARP and VAR.P ignore text and logical values in references. Please see VAR.P vs. VARPA for full details.
Variance formula in Excel - usage notes
To do variance analysis in Excel correctly, please follow these simple rules:
- Provide arguments as values, arrays, or cell references.
- In Excel 2007 and later, you can supply up to 255 arguments corresponding to a sample or population; in Excel 2003 and older - up to 30 arguments.
- To evaluate only numbers in references, ignoring empty cells, text, and the logical values, use the VAR or VAR.S function to calculate sample variance and VARP or VAR.P to find population variance.
- To evaluate logical and text values in references, use the VARA or VARPA function.
- Provide at least two numeric values to a sample variance formula and at least one numeric value to a population variance formula in Excel, otherwise a #DIV/0! error occurs.
- Arguments containing text that cannot be interpreted as numbers cause #VALUE! errors.
Variance vs. standard deviation in Excel
Variance is undoubtedly a useful concept in science, but it gives very little practical information. For instance, we found the ages of the population of tigers in a local zoo and calculated the variance, which equals 16. The question is - how can we actually use this number?
You can use variance to work out standard deviation, which is a much better measure of the amount of variation in a data set.
Standard deviation is calculated as the square root of the variance. So, we take the square root of 16 and get the standard deviation of 4.
In combination with the mean, the standard deviation can tell you how old most of the tigers are. For example, if the mean is 8 and the standard deviation is 4, the majority of the tigers in the zoo are between 4 years (8 - 4) and 12 years (8 + 4).
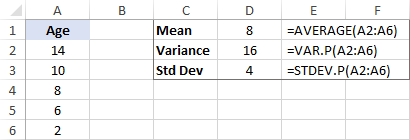
Microsoft Excel has special functions for working out standard deviation of a sample and population. The detailed explanation of all the functions can be found in this tutorial: How to calculate standard deviation in Excel.
That's how to do variance in Excel. To have a closer look at the formulas discussed in this tutorial, you are welcome to download our sample workbook at the end of this post. I thank you for reading and hope to see you on our blog next week!
Practice workbook
Calculate Variance in Excel - examples (.xlsx file)
 by
by
15 comments
Hi
What is the variance of this
FY 2023 FY2024 %Var F2023 vs F2024
March 347.37 329.82
April 346.49 335.33
May 250.96 449.97
June 318.42 344.19
July 325.34 349.84
August 304.88 339.96
Hi! Have you tried the ways described in this blog post? If they don’t work for you, then please describe your task in detail.
Target TY Sales LY Sales LW Sales Var TY Var LY Var LW LY % LW %
164 125.130 101.09 67.267 -38.870 -24.040 -57.863
How about when you have two columns, one for frequency & the other for quantity, what variance function would be applicable there? I have tried reformulating in every way - just to do the entire function manually.
This was super helpful!!
Extremely helpful - nicely explained
Extremely helpful - nicely put
Variance uses n-1 as a denominator, not n.
Very useful.
A very nice tips.
Thanks
I must have made an error with the age of tigers in the zoo example because my manually calculated variation matched your calculation of 16, but my Excel formula results were:
VAR = 20 {=VAR(Cell:cell)} even when {=VAR(14,10,8,6,2)} is used I still get 20.
VAR.S = 20
VARA = 20
VAR.P =16
Mean (avg) = 8
Standard Dev. = 4
The only reason I can deduce that I got 16 manually vice 20, as I did at first, is because I divided by 5 (population variance = n) instead of 4 (sample variance = n-1). So, I assume that this is a key difference to consider when selecting which Excel formula to use with a set.
Thank you. You've been very helpful.
Is there a way of calculating the variance in excel of a discrete probability distribution with just specifying the X values array & probability distribution array?
Thank you for the very useful and easy to understand lesson.