This is a short step-by-step tutorial for beginners showing how to add VBA code (Visual Basic for Applications code) to your Excel workbook and run this macro to solve your spreadsheet tasks.
Most people like me and you are not real Microsoft Office gurus. So, we may not know all specificities of calling this or that option, and we cannot tell the difference between VBA execution speed in different Excel versions. We use Excel as a tool for processing our applied data.
Suppose you need to change your data in some way. You googled a lot and found a VBA macro that solves your task. However, your knowledge of VBA leaves much to be desired. Feel free to study this step-by-step guide to be able to use the code you found:
Insert VBA code to Excel Workbook
For this example, we are going to use a VBA macro to remove line breaks from the current worksheet.
- Open your workbook in Excel.
- Press Alt + F11 to open Visual Basic Editor (VBE).
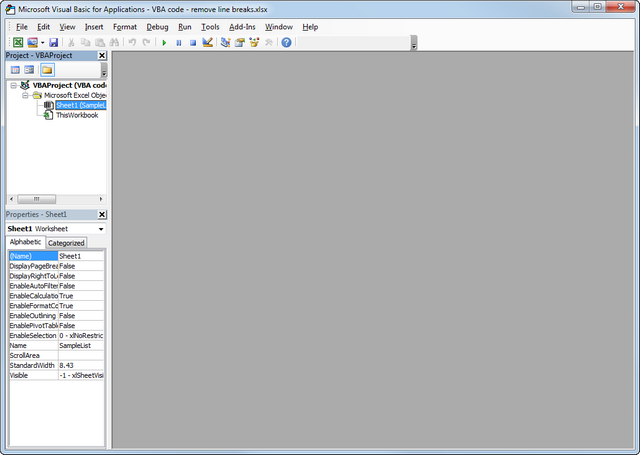
- Right-click on your workbook name in the "Project-VBAProject" pane (at the top left corner of the editor window) and select Insert -> Module from the context menu.
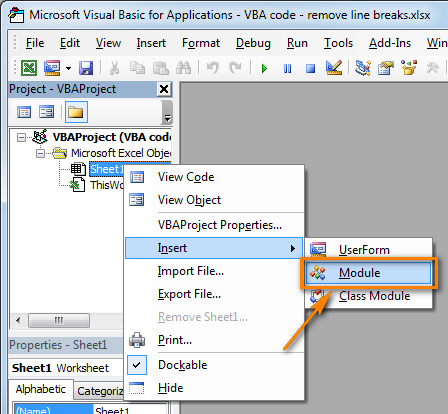
- Copy the VBA code (from a web-page etc.) and paste it to the right pane of the VBA editor ("Module1" window).
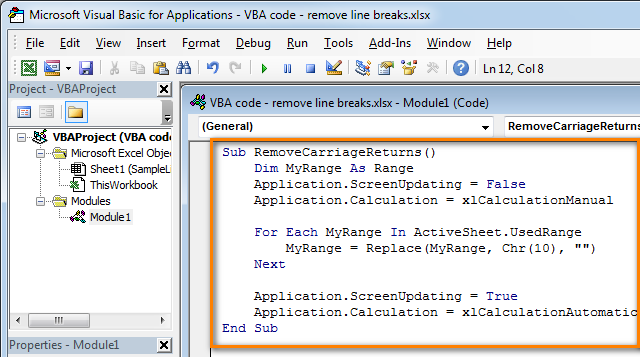
- Tip: Speed up macro execution
If the code of your VBA macro does not contain the following lines in the beginning:
Application.ScreenUpdating = False
Application.Calculation = xlCalculationManualThen add the following lines to get your macro to work faster (see the screenshots above):
- To the very beginning of the code, after all code lines that start with Dim (if there are no "Dim" lines, then add them right after the Sub line):
Application.ScreenUpdating = False
Application.Calculation = xlCalculationManual - To the very of the code, before End Sub:
Application.ScreenUpdating = True
Application.Calculation = xlCalculationAutomatic
These lines, as their names suggest, turn off screen refresh and recalculating the workbook's formulas before running the macro.
After the code is executed, everything is turned back on. As a result, the performance is increased from 10% to 500% (aha, the macro works 5 times faster if it continuously manipulates the cells' contents).
- To the very beginning of the code, after all code lines that start with Dim (if there are no "Dim" lines, then add them right after the Sub line):
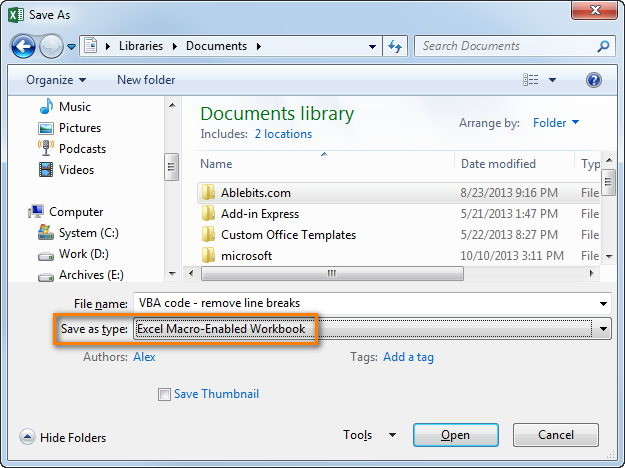
- Save your workbook as "Excel macro-enabled workbook".
Press Crl + S, then click the "No" button in the "The following features cannot be saved in macro-free workbook" warning dialog.

The "Save as" dialog will open. Choose "Excel macro-enabled workbook" from the "Save as type" drop-down list and click the Save button.
- Press Alt + Q to close the Editor window and switch back to your workbook.
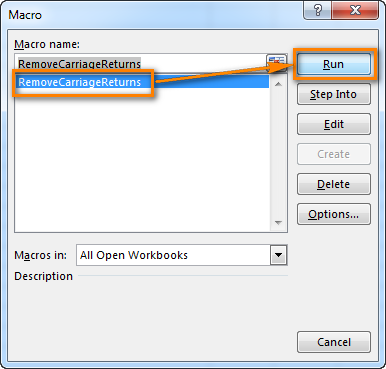
How to run VBA macros in Excel
When you want to run the VBA code that you added as described in the section above: press Alt+F8 to open the "Macro" dialog.
Then select the wanted macro from the "Macro Name" list and click the "Run" button.
 by
by
251 comments
hello dears ,
hope you're all doing well and safe , im very keen to know how can i generate VBA script to make my daily tasks easy please
i have an excel file generated from a specific app ( PPS ) , this excel show us where the shortages of products are ,
so we need to filter manual and do some formulas to know where first shortage is
can someone guide me and explain to me how to create VBA easy please ,
PS : i want to share with you the excel file but i didnt see any uploading button here ,
greetings,
Z.E
Hi! Your request goes beyond the advice we provide on this blog. We do not do VBA code creation on request.
Hi Alex ,
could you please guide me more or provide me an email box to share with you excel file for more clarification & understanding ,
thanks in advance Dear
Thank you
You say this is for beginners, but you use language that is for more experienced users. If it is for beginners, you need to include instructions for how to get to the things you are talking about, such as right click, left click, etc.
Hi! Unfortunately, this tutorial is for beginners to VBA, not for beginners to Excel.
Hi, my code was working previously but now isn't. I am not sure why. It gives me runtime error of 13
Sub Get_Plate_A_Data()
Dim FileToOpen As Variant
Dim OpenBook As Workbook
Application.ScreenUpdating = False
FileToOpen = Application.GetOpenFilename(Title:="Browse for your raw data file to import", FileFilter:="Excel Files (*.xls*), *xls*")
If FileToOpen False Then
Set OpenBook = Application.Workbooks.Open(FileToOpen)
OpenBook.Sheets(1).Range("C126:AP221").Copy
ThisWorkbook.Worksheets(Sheet1).Range("C39").PasteSpecial xlPasteValues
OpenBook.Close False
End If
Application.ScreenUpdating = True
End Sub
Hi! Your request goes beyond the advice we provide on this blog. We don't help with writing VBA code.
this feature is not available how to solve
Hi! I can't see your workbook, but perhaps these instructions will help you: How to enable and disable macros in Excel.
I’d like to take names from a column and have the entire row copied in a separate sheet.
Data example:
List of names in column D
If the name is “Cody Hall” then I want the entire row copied (not deleted) to a sheet named “Cody”
I’ve attempted to use VBA code to accomplish this but to no avail.
Hi! To get a row from the table based on the value in a column, you can try using the FILTER function. Read more: Excel FILTER function - dynamic filtering with formulas.
I want to delete A2 to A35 column using VB in excel, please help me
i'm a registered user of ablebits excel ultimate suite. is there a way to run a certain ablebits tool [in my case, transpose] from vba or in a recorded macro? if it is not possible, this would be great addition to the ultimate suite
Hi! Unfortunately, the capabilities of VBA do not allow you to do this.
Hey, can you tell me about the basis of VBA apply in Excel. I want to make my future in this field.
Hello, thank you for posting this. I'm currently trying to use it and I have followed the steps as written but when I go to the run the macro I get a syntax error on this line:
Set cellsColorSample = Application.InputBox( _
"Select sample color:", "Select a cell with sample color", _ Application.Selection.Address, Type:=8)
Any ideas what I need to change? I'm sorry but I know little of VB Scripting so I'm just trying to follow directions here. This is what I have:
Sub SumCountByConditionalFormat()
Application.ScreenUpdating = False
Application.Calculation = xlCalculationManual
Dim indRefColor As Long
Dim cellsColorSample As Range
Dim cntRes As Long
Dim sumRes
Dim cntCells As Long
Dim indCurCell As Long
On Error Resume Next
cntRes = 0
sumRes = 0
cntCells = Selection.CountLarge
Set cellsColorSample = Application.InputBox( _
"Select sample color:", "Select a cell with sample color", _ Application.Selection.Address, Type:=8)
If Not (cellsColorSample Is Nothing) Then
indRefColor = cellsColorSample.Cells(1, 1).DisplayFormat.Interior.Color
For indCurCell = 1 To (cntCells)
If indRefColor = Selection(indCurCell).DisplayFormat.Interior.Color Then
cntRes = cntRes + 1
sumRes = WorksheetFunction.Sum(Selection(indCurCell), sumRes)
End If
Next
MsgBox "Count=" & cntRes & vbCrLf & "Sum= " & sumRes & vbCrLf & vbCrLf & _
"Color=" & Left("000000", 6 - Len(Hex(indRefColor))) & _
Hex(indRefColor) & vbCrLf, , "Count & Sum by Conditional Format color"
End If
Application.ScreenUpdating = True
Application.Calculation = xlCalculationAutomatic
End Sub
I am trying to sum cells that are conditionally formatted red. Any help you can give would be GREATLY appreciated!!!
Hi! Copy the VBA code carefully from the article, or use the sample file linked at the end of the article.
Hi there, thanks for posting this. I'm currently trying to use it and have followed the steps as outlined but when I go to the run the macro there is nothing to select. Any idea why this might be?
Hi! If you have correctly inserted the macro code and saved the file correctly as described in the article above, try these guidelines: How to enable and disable macros in Excel.
Hello everyone, I would like to ask you for help with my problem. I think it's possible to solve it with VBA, but I'm not sure how to do it.
There is an application named Qtest. I want to link it with excel with the help of VBA macros , so that I can upload data from Excel to Qtest automatically.
Hi! Sorry, your request goes beyond the advice we provide on this blog.
I have an RFID reader putting value in active Excel cell. Then nothing more happenes, i want Excel to automaticly move active cell to the cell below and calculate the sheet :-(
Hi! Unfortunately, I cannot reproduce your problem. Set the cursor to move automatically after entering a value in a cell: Options - Advanced - Editing options. Also check in the menu on the ribbon: Formulas - Calculation options - Automatic.
Add to VBA code the first executable statement: Application.Volatile.
I was able to do this using Office 2003, but after closing and then opening, i get the message that my VB project was removed. Ive spent hrs googling and experimenting but I cant find the solution. I have no problems if I use Office 2013, unfortunately, the old program im using will not work with newer versions of excel. Any ideas?
Unfortunately, code created in Excel 2013 and later does not work in Excel 2003.
Im not using excel 2013, im trying to get excel 2003 to stop removing my macro after closing/opening. I meant my old lintool program will not work with new versions of excel so im stuck using the 2003 excel.
Unfortunately, your old program doesn't work with modern VBA macros.
Thanks so much Alexander! that is very helpful.
Fails at Step 2. When I Press Alt-F11, I get the editor screen, but not the left-hand panel shown in the image. :-(.
Press Ctrl + R
This is so good & helpful for first time user like me - Thanks so much
Can someone help me with the following script? There is something wrong with the last call function of this.
Sub Admin()
' Defines variables
Dim Cell As Range, sRange As Range, Rng As Range
' Defines LastCol as the last column with a header on the Run sheet
LastCol = Sheets("SABER").Cells(1, Columns.Count).End(xlToLeft).Column
' Sets the search range as A1 to the last column with a header on the Run sheet
Set sRange = Sheets("SABER").Range("A1", Cells(1, LastCol))
' With the search range
With sRange
' Set Rng as the cell where "Admin No." is found
Set Rng = .Find(What:="Admin No.", _
After:=.Cells(1), _
LookIn:=xlValues, _
LookAt:=xlWhole, _
SearchOrder:=xlByRows, _
SearchDirection:=xlPrevious, _
MatchCase:=False)
' If Rng exists then
If Not Rng Is Nothing Then
' Define LastRow as the last row of data under the Due Date header
lastRow = Sheets("SABER").Cells(Rows.Count, Rng.Column).End(xlUp).Row
' Copy from the Systme Consition header down to the last row of that column and paste to A1 of Paste Report Here sheet
Sheets("SABER").Range(Rng, Cells(lastRow, Rng.Column)).Copy _
Destination:=Sheets("Status").Range("A1")
End If
End With
End Sub
What I'm trying to accomplish here is to display the "Admin No." Column from sheet 3 "Saber" (no matte where it is in sheet 3) to a sheet called "Status".
This works really well HOWEVER The issue is when a row is deleted from Saber and I run the Macro in status the row remains where there like I never deleted it.
Any help would be apricated.
Dose anyone one know if the above process can be accomplished without the Marco? ie. search sheet 2 for a certain column regardless of where it is and populate it in sheet 1.
We apologize, but we cannot offer assistance beyond the scope of this blog.
I am trying to create a macro that will unlock a worksheet and spellcheck the sheet and lock the worksheet again. But I also want to still be able to format rows. When I use the generic macro I found online it defaults to not allowing the worksheet to allow for row formatting? And when I try to use the record macro function to do the same functions it want the password and leaves it protected with no password. Does anybody have a solution?
I want to creat a sequence from 1 to infonity and skip all ending zero number such that 10,20,30,.... Also no skip any indices
Hello can VBA code be inserted into Excel 365? if so how?
Hi!
You can record and run VBA macros with all Excel desktop versions. In the online version of Excel, VBA does not work.
Hi,
I'm trying to add a blank row between every row.
After running the VBA code, I get an error 6 - overflow.
When debugging, it looks like there's an issue with the following string:
CountRow = rng.EntireRow.Count
Please help me resolve this <3
Hello,
I need to use VBA in a worksheet_change event instead of formula, so you can leave the cell empty ready for user interface, or when the conditions are met the value can be put in the cell automatically and protected at the same time. I am looking to autopopulate previously entered data based on the client's unique identifier. This is my formula, which works/allows for the formula to auto-populate/return data BUT it doesn not allow for data entry if there is no match/data to return once the sheet is protected?
=IFERROR(INDEX($C$7:C7,MATCH($A$7:$A$6001,$A$7:$A$6001,0))," ")
Hi!
Unfortunately, here we can only help you with Excel formulas.
Hi, I'm looking for a solution that create a button to print excel worksheet with print range A2:AA73 from a workbook into pdf and save a copy of pdf in specific file location and file name will be based on each sheet cell value at AD2
Can you help me with how to code that part? I'll be really appreciated your help.
Hi everyone,
can you please help me on writing VBA code in excel as per my requirement:
Requirement:
In Cell: D23 (containing formula value automatically generated on every 15 minutes)
In column c23=current time value is showing
In Cell "A30:A54" (value started from 9.30, 9.15, 10.00, 10.15, 10.30, 10.45, 12.00, 12.15, 12.30, 12.45, 13.00, 13.15, 13.30, 13.45, 14.00, 14.15, 14.30, 14.45, 15.00, 15.15, 15.30 respecitively each time value in each row)
Now I want to copy cell D23 value and Paste value only inside the Cell Range : B30:B54 where Cell C23=matches with Cell A30:A54).
Kindly help to write code on VBA in excel.
Thank you very much
thanks
Hi, I'm looking for a solution that is I created a report on excel and I also created a button to export that report excel file into a pdf and its location is on Sharepoint, not in some folder only on Computer. Can you help me with how to code that part? I'll be really appreciated your help.
Is there a code set or technique to get an excel sheet to read all the documents in a folder, their headers (if they are word documents) and then build a hyperlink list with colums that display data fields from the header like dates/vital-info/etc.
Is this possible?
Hi
Is there a code or tool in Excel to enable a cell pop up a number previously entered in another cell immediately that number is deleted?
I've written a whole script which works in extracting all the information from a Questionnaire in word to excel. However, the only problem I've run into is when questions within the Questionnaire has tick box options. My current VB macro script just pulls in the box symbol, but not the words associated with the ticked box/next to the tick boxes. Is there a VB macro script you can recommend I can write which allows me to pick up the text associated with the ticked box instead?
Hello,
I need to learn coding in excell. Actually I want to use coding in excell for getting expenditures year wise. In excell sheet im going to fill cells with expenditures pertain to different years but i want excell to use codes and give those expenditures years wise as an easy reporting. Kindly guide me through this how could i get desired results, please.
I have 2 Dropdown List with the same options (Included and Excluded) in different sheets. If I select " Included" in one dropdown list, it should also select "Included" on another dropdown list and vice versa. I need VBA code to crack this.
I have an excel excel workbook .It has four sheets A, B, C, D .A, sheet information .Rowes' information is categorized in C column. VBA code so that the information contained in the Rowes can be found on the B sheet, the information on the C on the C sheet and the information on the D on the D sheet. want to .
Hi
I have 3 sheets work book. sheet1 'E,sheet 2 'N anf Sheet 3 'D'. It has 1000 rows in sheet 1. "H" column data catagary 'N' and 'D' two data type .I want to link data by N or D to other two sheets .
this deleted active names as well so my entire excel has #name error now. is there a VBA that only deleted names that are not used
I am having an excel wherein i have done some conditional formatting with color coding and i just want to copy the color codes to another fields, can you suggest a macro VBA so that i can run it?
Hi
May I request the expertise of those who are professionals in VBA. I'm planning to improve my procurement monitoring in excel using the VBA wherein I want to simplify the way I can search for the status of purchases. By simply typing the reference number in the search bar then the status would appear. Would that be possible in excel VBA. Thank you in advance for your help
how i can give command in execel
Hi,
I need a code to color the sheet tab to red if T43 in that sheet is > 0, no change to sheet color for all other cases. I'd like this to run for the entire workbook of 160 sheets automatically. Can someone help?
Thank you.
Alice
i like your question as well.
Can someone help us on this?
Hi!
Unfortunately, we can't help writing a VBA macro. Only Excel formulas.
please can I have a cod to calculate the average for each 29 number of excel column with 184450 row
Hello everyone, I would like to ask you for help with my problem. I think it's possible to solve it with VBA, but I'm not sure how to do it. Also, if there is a way to do it without VBA, even better.
I exported the tasks from the Planner to Excel (did some work to filter and format the data I needed, etc.) and finally, I have a list of tasks that belong to a person. For each person, I have to manually enter the approximate time needed to complete the task, during the task that person should enter each week how many hours he spends solving the task and when the task is completed I can compare in the table the time he spends and the time I set for this assignment. This table needs to be used for a long time, and the task list changes almost every week, so I need to export new data from the scheduler every week, but save the data previously entered for some tasks. Each time an export is performed, the order of tasks in Excel changes and this is the point when a problem occurs. The time I need to specify for each task (forecast) is entered manually, for example, for the task "Task1" in A1 the forecast is entered in C1. The next time I export tasks from the Planner, it is possible that "Task 1" will no longer be in A1 (ie I added another task in the Planner and now that task is the first, so "Task 1" moves to A2), but the forecast for " Task 1 "remained in C1 (because column C is not included in exports). How to ensure that cell C1 follows the task in A1, no matter where the data from A1 is transferred? In this case, when a new export is made, the forecast from C1 should be automatically moved to C2, because the task from A1 is now to A2. I hope someone can help me. Thanks in advance, Los
I Want use VBA code flash data on return on blog
Hello, thank you for your help. If possible, could you please help me with an additional problem? I have around 1000+ xml files and I want to convert them to excel or csv file. Is it possible to do that as well? If so, can you show me how?
Thank you for your time.
Hey! I am looking for a little help with a code. I am a beginner it is a little confusing..
Change the application so that now there is no limit.
For EG, if the strategy says to buy 30% more shares but there is not enough cash on hand to do so, the investor will now borrow the cash they need. Now the cash positions in
columns H and J of the Model worksheet can be negative, indicating that the investor
owes money to the lender.
Capture the maximum the investor ever owes during the year in an extra output cell, keep
track of it, and summarize it (including a histogram), just like all of the other outputs,
with your VBA code.
Hi Sir i want to count diffent names in coloum wise what is the formula or code?
i am new vb in excel and need some assistance with the following macro. any help greatly appreciated. i need to create a macro which will take value from sheet 1 cell A1 value ,(example: CD-600500 is available in sheet 1 cell A1) then increment the value by 1 in sheet 2 cell range A5:A50,also A5:A50 if the cell is blank try goto next row and increment the value by 1.
I need a code to convert half of my numbers to variables. example if the number is 12345, i need to convert it as ABC45. (A=1, B=2 Etc..) Someone Please help.
hi there, im quite new at programming but uses excel alot so what im looking for would help me quite alot.
i would like to create a macro or a button that takes the value i a cell and multiplies it with negative one.
Example:
i have multiple sheets and plots in a number from sheet one to sheet two, then in sheet two i need the number to be multiplied with negative one, whilst still being traceble to where the value came from. is this possible?
sorry if the explenation is bad, English is my second language.