How to use Solver in Excel with examples
The tutorial explains how to add and where to find Solver in different Excel versions, from 2016 to 2003. Step-by-step examples show how to use Excel Solver to find optimal solutions for linear programming and other kinds of problems.
Everyone knows that Microsoft Excel contains a lot of useful functions and powerful tools that can save you hours of calculations. But did you know that it also has a tool that can help you find optimal solutions for decision problems?
In this tutorial, we are going to cover all essential aspects of the Excel Solver add-in and provide a step-by-step guide on how to use it most effectively.
What is Excel Solver?
Excel Solver belongs to a special set of commands often referred to as What-if Analysis Tools. It is primarily purposed for simulation and optimization of various business and engineering models.
The Excel Solver add-in is especially useful for solving linear programming problems, aka linear optimization problems, and therefore is sometimes called a linear programming solver. Apart from that, it can handle smooth nonlinear and non-smooth problems. Please see Excel Solver algorithms for more details.
While Solver can't crack every possible problem, it is really helpful when dealing with all kinds of optimization problems where you need to make the best decision. For example, it can help you maximize the return of investment, choose the optimal budget for your advertising campaign, make the best work schedule for your employees, minimize the delivery costs, and so on.
How to add Solver to Excel
The Solver add-in is included with all versions of Microsoft Excel beginning with 2003, but it is not enabled by default.
To add Solver to your Excel, perform the following steps:
- In Excel 2010, Excel 2013, Excel 2016, and Excel 2019, click File > Options.
In Excel 2007, click the Microsoft Office button, and then click Excel Options. - In the Excel Options dialog, click Add-Ins on the left sidebar, make sure Excel Add-ins is selected in the Manage box at the bottom of the window, and click Go.
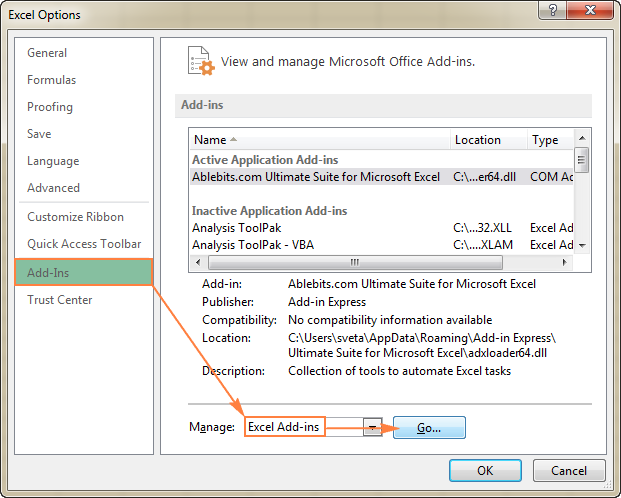
- In the Add-Ins dialog box, check the Solver Add-in box, and click OK:
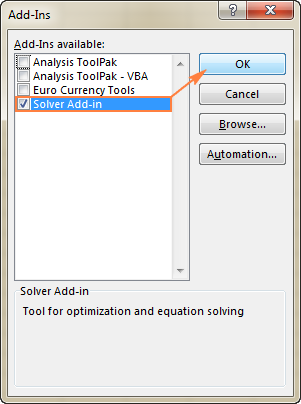
To get Solver on Excel 2003, go to the Tools menu, and click Add-Ins. In the Add-Ins available list, check the Solver Add-in box, and click OK.
Where is Solver in Excel 2019, 2016, 2013, 2010 or 2007?
In the modern versions of Excel, the Solver button appears on the Data tab, in the Analysis group:
Where is Solver in Excel 2003?
After the Solver Add-in is loaded to Excel 2003, its command is added to the Tools menu:
Now that you know where to find Solver in Excel, open a new worksheet and let's get started!
How to use Solver in Excel
Before running the Excel Solver add-in, formulate the model you want to solve in a worksheet. In this example, let's find a solution for the following simple optimization problem.
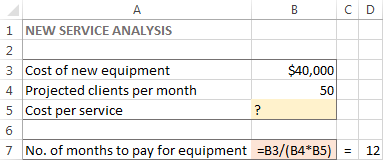
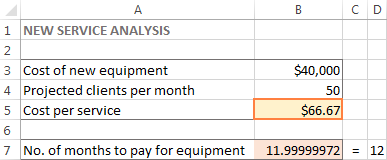
Problem. Supposing, you are the owner of a beauty salon and you are planning on providing a new service to your clients. For this, you need to buy a new equipment that costs $40,000, which should be paid by instalments within 12 months.
Goal: Calculate the minimal cost per service that will let you pay for the new equipment within the specified timeframe.
For this task, I've created the following model:
And now, let's see how Excel Solver can find a solution for this problem.
1. Run Excel Solver
On the Data tab, in the Analysis group, click the Solver button.
2. Define the problem
The Solver Parameters window will open where you have to set up the 3 primary components:
- Objective cell
- Variable cells
- Constraints
Exactly what does Excel Solver do with the above parameters? It finds the optimal value (maximum, minimum or specified) for the formula in the Objective cell by changing the values in the Variable cells, and subject to limitations in the Constraints cells.
Objective
The Objective cell (Target cell in earlier Excel versions) is the cell containing a formula that represents the objective, or goal, of the problem. The objective can be to maximize, minimize, or achieve some target value.
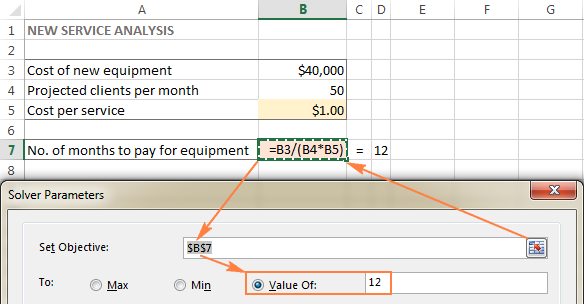
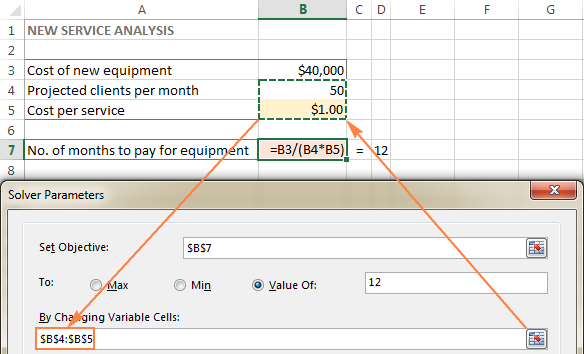
In this example, the objective cell is B7, which calculates the payment term using the formula =B3/(B4*B5) and the result of the formula should be equal to 12:
Variable cells
Variable cells (Changing cells or Adjustable cells in earlier versions) are cells that contain variable data that can be changed to achieve the objective. Excel Solver allows specifying up to 200 variable cells.
In this example, we have a couple of cells whose values can be changed:
- Projected clients per month (B4) that should be less than or equal to 50; and
- Cost per service (B5) that we want Excel Solver to calculate.
Constraints
The Excel Solver Constrains are restrictions or limits of the possible solutions to the problem. To put it differently, constraints are the conditions that must be met.
To add a constraint(s), do the following:
- Click the Add button right to the "Subject to the Constraints" box.
- In the Constraint window, enter a constraint.
- Click the Add button to add the constraint to the list.
- Continue entering other constraints.
- After you have entered the final constraint, click OK to return to the main Solver Parameters window.
Excel Solver allows specifying the following relationships between the referenced cell and the constraint.
- Less than or equal to, equal to, and greater than or equal to. You set these relationships by selecting a cell in the Cell Reference box, choosing one of the following signs: <=, =, or >=, and then typing a number, cell reference / cell name, or formula in the Constraint box (please see the above screenshot).
- Integer. If the referenced cell must be an integer, select int, and the word integer will appear in the Constraint box.
- Different values. If each cell in the referenced range must contain a different value, select dif, and the word AllDifferent will appear in the Constraint box.
- Binary. If you want to limit a referenced cell either to 0 or 1, select bin, and the word binary will appear in the Constraint box.
To edit or delete an existing constraint do the following:
- In the Solver Parameters dialog box, click the constraint.
- To modify the selected constraint, click Change and make the changes you want.
- To delete the constraint, click the Delete button.
In this example, the constraints are:
- B3=40000 - cost of the new equipment is $40,000.
- B4<=50 - the number of projected patients per month in under 50.
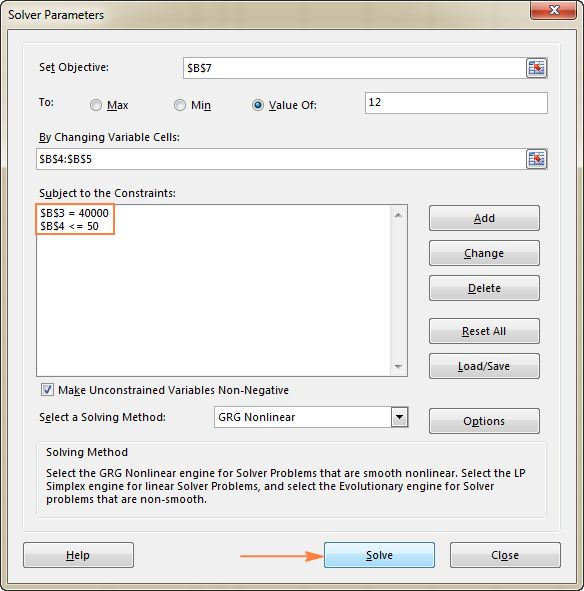
3. Solve the problem
After you've configured all the parameters, click the Solve button at the bottom of the Solver Parameters window (see the screenshot above) and let the Excel Solver add-in find the optimal solution for your problem.
Depending on the model complexity, computer memory and processor speed, it may take a few seconds, a few minutes, or even a few hours.
When Solver has finished processing, it will display the Solver Results dialog window, where you select Keep the Solver Solution and click OK:
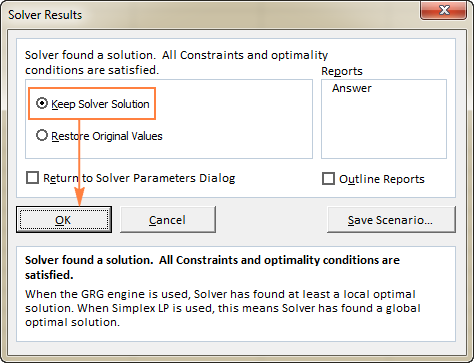
The Solver Result window will close and the solution will appear on the worksheet right away.
In this example, $66.67 appears in cell B5, which is the minimal cost per service that will let you pay for the new equipment in 12 months, provided there are at least 50 clients per month:
- If the Excel Solver has been processing a certain problem for too long, you can interrupt the process by pressing the Esc key. Excel will recalculate the worksheet with the last values found for the Variable cells.
- To get more details about the solved problem, click a report type in the Reports box, and then click OK. The report will be created on a new worksheet:
Now that you've got the basic idea of how to use Solver in Excel, let's have a closer look at a couple more examples that might help you gain more understanding.
Excel Solver examples
Below you will find two more examples of using the Excel Solver addin. First, we will find a solution for a well-known puzzle, and then solve a real-life linear programming problem.
Excel Solver example 1 (magic square)
I believe everyone is familiar with "magic square" puzzles where you have to put a set of numbers in a square so that all rows, columns and diagonals add up to a certain number.
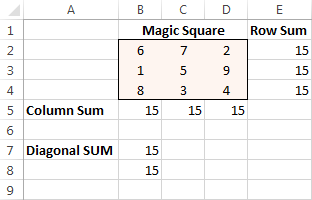
For instance, do you know a solution for the 3x3 square containing numbers from 1 to 9 where each row, column and diagonal adds up to 15?
It's probably no big deal to solve this puzzle by trial and error, but I bet the Solver will find the solution faster. Our part of the job is to properly define the problem.
To begin with, enter the numbers from 1 to 9 in a table consisting of 3 rows and 3 columns. The Excel Solver does not actually need those numbers, but they will help us visualize the problem. What the Excel Solver add-in really needs are the SUM formulas that total each row, column and 2 diagonals:
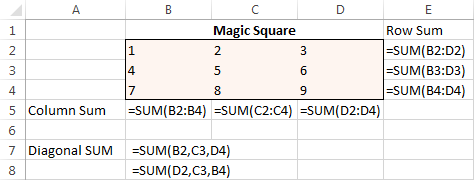
With all the formulas in place, run Solver and set up the following parameters:
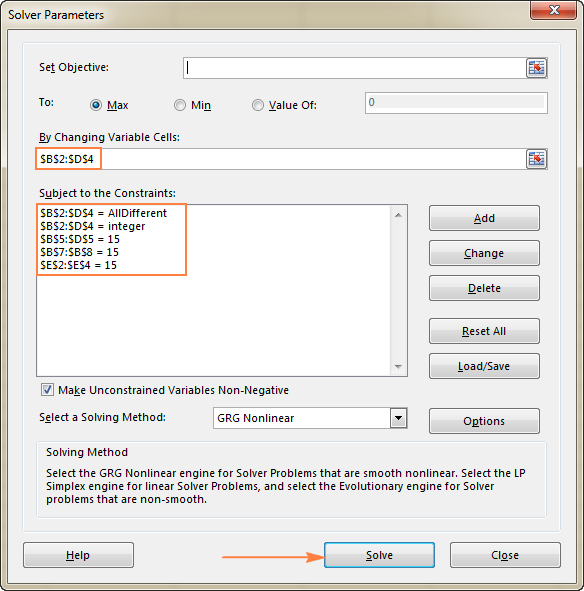
- Set Objective. In this example, we don't need to set any objective, so leave this box empty.
- Variable Cells. We want to populate numbers in cells B2 to D4, so select the range B2:D4.
- Constraints. The following conditions should be met:
- $B$2:$D$4 = AllDifferent - all of the Variable cells should contain different values.
- $B$2:$D$4 = integer - all of the Variable cells should be integers.
- $B$5:$D$5 = 15 - the sum of values in each column should equal 15.
- $E$2:$E$4 = 15 - the sum of values in each row should equal 15.
- $B$7:$B$8 = 15 - the sum of both diagonals should equal 15.
Finally, click the Solve button, and the solution is there!
Excel Solver example 2 (linear programming problem)
This is an example of a simple transportation optimization problem with a linear objective. More complex optimization models of this kind are used by many companies to save thousands of dollars each year.
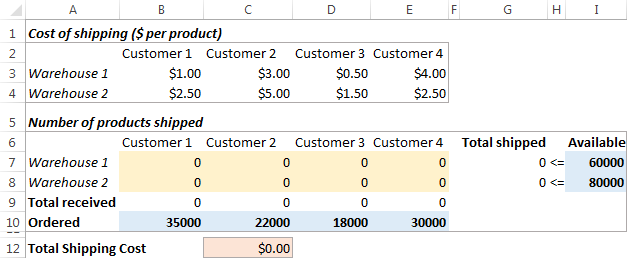
Problem: You want to minimize the cost of shipping goods from 2 different warehouses to 4 different customers. Each warehouse has a limited supply and each customer has a certain demand.
Goal: Minimize the total shipping cost, not exceeding the quantity available at each warehouse, and meeting the demand of each customer.
Source data
Here is how our transportation optimization problem looks like:
Formulating the model
To define our linear programming problem for the Excel Solver, let's answer the 3 main questions:
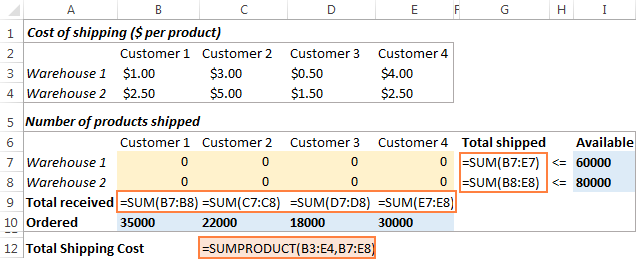
- What decisions are to be made? We want to calculate the optimal quantity of goods to deliver to each customer from each warehouse. These are Variable cells (B7:E8).
- What are the constraints? The supplies available at each warehouse (I7:I8) cannot be exceeded, and the quantity ordered by each customer (B10:E10) should be delivered. These are Constrained cells.
- What is the goal? The minimal total cost of shipping. And this is our Objective cell (C12).
The next thing for you to do is to calculate the total quantity shipped from each warehouse (G7:G8), and the total goods received by each customer (B9:E9). You can do this with simple Sum formulas demonstrated in the below screenshot. Also, insert the SUMPRODUCT formula in C12 to calculate the total cost of shipping:
To make our transportation optimization model easier to understand, create the following named ranges:
| Range name | Cells | Solver parameter |
| Products_shipped | B7:E8 | Variable cells |
| Available | I7:I8 | Constraint |
| Total_shipped | G7:G8 | Constraint |
| Ordered | B10:E10 | Constraint |
| Total_received | B9:E9 | Constraint |
| Shipping_cost | C12 | Objective |
The last thing left for you to do is configure the Excel Solver parameters:
- Objective: Shipping_cost set to Min
- Variable cells: Products_shipped
- Constraints: Total_received = Ordered and Total_shipped <= Available
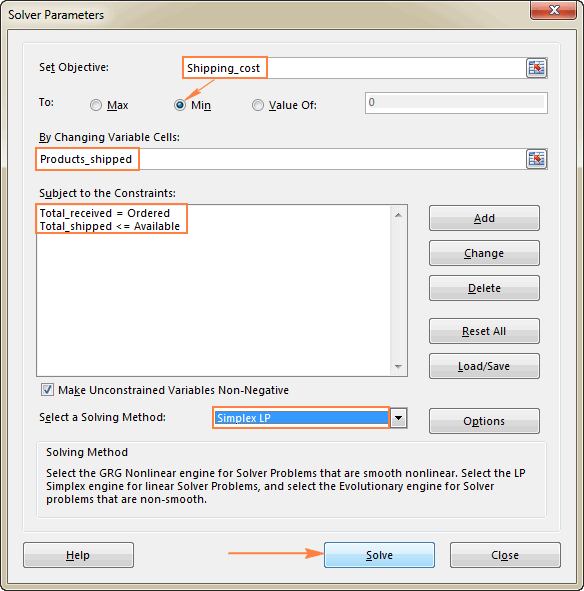
Please pay attention that we've chosen the Simplex LP solving method in this example because we are dealing with the linear programming problem. If you are not sure what kind of problem yours is, you can leave the default GRG Nonlinear solving method. For more information, please see Excel Solver algorithms.
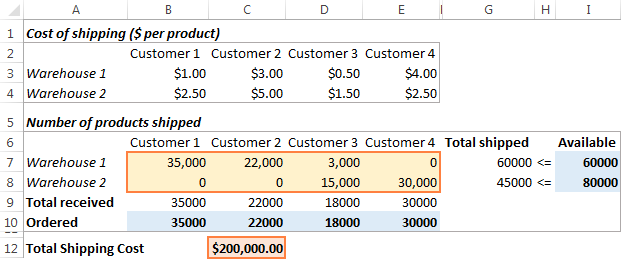
Solution
Click the Solve button at the bottom of the Solver Parameters window, and you will get your answer. In this example, the Excel Solver add-in calculated the optimal quantity of goods to deliver to each customer from each warehouse with the minimal total cost of shipping:
How to save and load Excel Solver scenarios
When solving a certain model, you may want to save your Variable cell values as a scenario that you can view or re-use later.
For example, when calculating the minimal service cost in the very first example discussed in this tutorial, you may want to try different numbers of projected clients per month and see how that affects the service cost. At that, you may want to save the most probable scenario you've already calculated and restore it at any moment.
Saving an Excel Solver scenario boils down to selecting a range of cells to save the data in. Loading a Solver model is just a matter of providing Excel with the range of cells where your model is saved. The detailed steps follow below.
Saving the model
To save the Excel Solver scenario, perform the following steps:
- Open the worksheet with the calculated model and run the Excel Solver.
- In the Solver Parameters window, click the Load/Save button.
- Excel Solver will tell you how many cells are needed to save your scenario. Select that many empty cells and click Save:
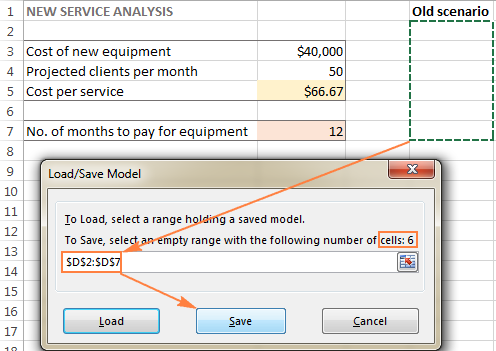
- Excel will save your current model, which may look something similar to this:
At the same time, the Solver Parameters window will show up where you can change your constraints and try different "what if" options.
Loading the saved model
When you decide to restore the saved scenario, do the following:
- In the Solver Parameters window, click the Load/Save button.
- On the worksheet, select the range of cells holding the saved model and click Load:
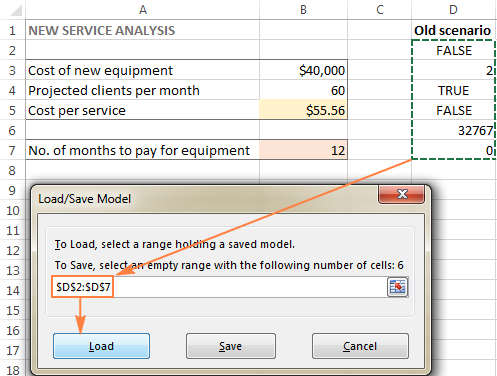
- In the Load Model dialog, click the Replace button:
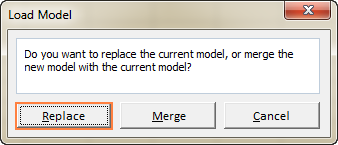
- This will open the main Excel Solver window with the parameters of the previously saved model. All you need to do is to click the Solve button to re-calculate it.
Excel Solver algorithms
When defining a problem for the Excel Solver, you can choose one of the following methods in the Select a Solving Method dropdown box:
To change how Solver finds a solution, click the Options button in the Solver Parameters dialog box, and configure any or all options on the GRG Nonlinear, All Methods, and Evolutionary tabs.
This is how you can use Solver in Excel to find the best solutions for your decision problems. And now, you may want to download the Excel Solver examples discussed in this tutorial and reverse-engineer them for better understanding. I thank you for reading and hope to see you on our blog next week.
26 Responses to "How to use Solver in Excel with examples"
Awesome knowledge
Keep it up
AbleBits team,
Thank you sir a wonderful article
Thanks for such a nice & easy tutorial of difficult commands.
excellent tutorial
Excellent & very descriptive examples
thanks
Great explanation! Thorough Demonstration of Skills and a brilliant performance
Thank you there is no things more than this to upload your knowledge
Many thanks I have been trying to learn this function for decades.
hello,
please i was giving this assignment but i am finding it hard to understand it. please can any one help me solve it?
To create a Linear Programming model using MS Excel Solver (25%)
A metal works manufacturing company produces four products fabricated from sheet metal in a
production line that consist of four operations: 1) Stamping, 2) Assembly, 3) Finishing and 4)
Packaging. The processing times per unit for each operation and total available hours per month
are as follows:
Product (hour/unit)
Operation 1 2 3 4 Total Hours available per
month
Stamping 0.07 0.2 0.1 0.15 700
Assembly 0.15 0.18 -- 0.12 450
Finishing 0.08 0.21 0.06 0.10 600
Packaging 0.12 0.15 0.08 0.12 500
5
The sheet metal required for each product, the maximum demand per month, the minimum
required contracted production, and the profit per product are given as follows:
Monthly sales demand
Product Sheet Metal (ft2
) Minimum Maximum Profit(£)
1 2.1 300 3,000 9
2 1.5 200 1,400 10
3 2.8 400 4,200 8
4 3.1 300 1,800 12
The company has 5,200 square feet of fabricated metal available each month.
Formulate a linear programming model and use Excel Solver function to suggest the best mix of
products which would result in the highest profit within the given constraints.
Can u better rephrase or construct the question properly
Hello Charles,
I managed to solve the problem that you posted (albeit some understandings I have changed to suit the scenario). Post your email ID and I will post the excel file to you asap.
Warm Regards,
Bhupesh
i faced a problem with exelsolver by error how can i correct that?
Excellent Sir, thanks a lot.
Question? I created a workbook for scheduling hours for employees working at a movie theater for 1 week. I need to have a certain number of employees for each day of the week, but I need to deal with their timeoff requests. And some of my employees are fulltime and some parttime. The timeoff request says "Can't work Saturday". I need to write a constraint based on those entries, add constraints so that employees are not scheduled to work on days when they are unavailable to work. How do I write a constraint to cover this?
Great. Everything that I wanted to know more about solver is here.
Fantastic Examples to make you understand the algorithm.
You explain very well! You have a gift
Dear Cheusheva
I have tried my best to study your instruction and practice with my problem but I fail to come to an acceptable result.
I hope you help me.
I have a table as follows
x1 x2 x3 x4 Age Code Name
34 36 38 42 17 0 A
32 38 40 41 19 1 B
36 39 32 40 20 0 C
42 34 42 41 19 1 D
33 38 42 29 20 1 E
31 39 41 45 18 0 F
(others in similar form)
I want to have a minimum of sum of four variables with the constraints
- A person (name) is chosen only 1 time in the sum (4 people for four variables)
- Sum of code is 2 (two "1" and two "0")
- sum of age is <=60
I hope to have your reply soon.
Best regards
Hi. I’m very new to solver and was asked to solve this question:
Mathew is the business owner of a laundry shop located at City Plaza. He has operated the
business since June 2018 and after operating it for 6 months, he has realised that in certain
months, the sales revenue is sufficient to cover the operating expenditures, while for certain
months the sales revenue is not enough to cover the operating expenditures and he has to rely
on his personal savings to tide through.
It is now the last week of December 2018 and he realises that moving forward, it is better for
his business to have access to loan facility from the bank to ease out his operation. However,
he is unsure of which loan package to sign up and has approached you, a close friend, to help
him as you are trained in financial planning. To perform the analysis, you have requested
Mathew to give a projection of the sales revenue and operating expenditures for the next
twelve months. The estimates are as follows:
Month Sales Revenue ($) Bills ($)
January 4,000 6,000
February 3,000 5,000
March 3,000 4,000
April 3,000 3,000
May 5,000 4,000
June 9,000 1,000
July 3,000 6,000
August 2,000 6,000
September 1,000 4,000
October 2,000 2,000
November 6,000 1,000
December 10,000 1,000
Based on the whole year projection, Mathew will make $8,000 net profit at the end of the
year. However, since all expenditures must be paid in full by the end of every month,
Mathew may be short on cash in some months until he sees the big sales in certain months,
e.g. June and December. Mathew has two sources of loan:
Annual loan at 12% of interest per year, e.g. he borrows $100 at the beginning of
January 2019 and pays back $112 at the end of December 2019. Early-pay-back is not
allowed and Mathew can get an annual loan in January only.
Monthly loan at 2.5% of interest, e.g. he borrows $100 at the end of March and pays
back $102.5 at the end of April. Early-pay-back is not allowed and Mathew cannot get
a monthly loan in December.
He needs your help to determine whether he should just take up the annual loan with effect
from January, or a mixture of both types of loan facilities. Assume that Mathew has zero cash
balance at the beginning of 2019.
I have tried to look up similar questions online but the prob is I don’t understand how the solution was derived. Can someone help please? Thank you.
I tried the Magic Square one with my students and we were not able to solve it as directed. We received error messages, such as "An AllDifferent Constraint must have either no bounds, or a lower bound of 1 and and upper bound of N, where N is the number of cells in the Constraint." However, we could not figure out where to set this parameter.
Can anyone help with this?
Hi Michelle,
To figure out the source of the problem, you can download our sample workbook and compare our Magic Square model with yours.
Hello there!
I have a problem with production scheduling.
We have three wire cutting machines and 90 different tools for contactor crimping and seal application (automotive harness business) that are being used on these machines as active processing parts for the different wires and other harness components. Operation on each of the machine is similar except that combination of tools is different, first the machine unroll the wire form the spool, then it cuts the wire on a predetermined length, then applies a seal (water protection) and then crimp a contactor. There are operations where we use two seal applicators and crimping tools on a single machine, so both ends of the wire are sealed and crimped. The combination depends on the wire cross-section, seal specification and contactor specification (crimp parameters vary based on the client specification). Goal - is to prepare the production plan with minimum change over of the tools and eliminate the situations when the tools are needed on more than one machine. The replanting has to be flexible, even daily. Some tools are available in more than one unit (two three). The changeover of applicators is longer than for crimping tools (1.5 hours vs. 30 min). Would be good to have a tip how to solve this complex task.
Look forward to hear from you!
Slava
Hi everyone, i am Silvana Pantic, from Slovenia, am so glade coming back to this great forum to testify about the help i received from Credit-Suisse Loan Film. I was in desperate need of a loan in other to be free from debt and financial bondage that was place on me by my ex husband. It was really bad that i have to seek for help from Friends,family and even my bank but on one could assist me because my credit score was really bad. So i was browsing with my computer and saw some testimonies from people that Credit-Suisse Loan Film assisted with a loan, then i decided to contact them via email {credit-suisse147@hotmail.com}
A theatre company needs to determine the lowest cost production budget for an upcoming theatre show. Specifically, they will have to determine the lowest which set pieces to construct and which pieces must be rented from another company at a pre-determined fee. The time available for constructing the set is two weeks after which rehearsals commence. To construct the set, the theatre has two part-time carpenters who work upto 12 hours a week and each at $100 per hour. Additionally, the scene artist can work 15 hours per week at $150 per hour.
The set design requires 20 walls, 2 hanging drops with pained scenery and 3 large wooden tables serving as props. The number of hours required for each piece for carpentry and painting is given below.
Carpentery Painting
Walls 0.5 2.0
Hanging Drops 2.0 3.0
Wooden Tables 3.0 4.0
Flats, hanging drops and props can also be rented at a cost of $750, $5000 and $3500 each. How many of each unit should be built by the theatre company and how many units should be rented to minimize costs?
Very nice tutorial. Lot of thanks.
Good work